 |
LandscapeDNDC
1.37.0
|
 |
LandscapeDNDC
1.37.0
|
MeTrx simulates carbon and nitrogen cycle of soils. Focus lies on the production and consumption of the greenhouse gases \( CO_2, CH_4 \) and \( N_2O \). Therewith related outputs include leaching of \( NO_3 \) and emissions of \( NH_3 \). Depending on the ecosystem of interest, several model options should be considered (see also: metrxoptions):
Microbial processes are especially relevant in the upper soil layers. Choose a spatial discretization of at maximum 0.5 cm for the upper 1cm soil depth. For a soil depth greater 1cm and smaller 10 cm, a spatal discretization of 1-2 cm per soil layer is recommended.
MeTrx requires further models for:
MeTrx includes the following siteparameters:
The calibration of nitrogen trace gas emissions primarily addresses microbial metabolism, anaerobic conditions, and transport. The processes of decomposition and humification of SOM should be excluded or managed carefully in order to avoid compromising the overall stability of SOM by inadvertently inducing unrealistically high losses or gains.
| name | mean | min | max | coderef | calibration_target |
|---|---|---|---|---|---|
| METRX_MUEMAX_C_MIC | 5 | 3 | 7 | Microbial dynamics | SOC |
| METRX_AMAX | 1 | 0.5 | 1.5 | Microbial dynamics | N2O,SOC |
| METRX_F_MIC_T_EXP_1 | 3.5 | 2 | 5 | Temperature and moisture dependency of microbial growth | N2O,SOC |
| METRX_F_MIC_T_EXP_2 | 35 | 25 | 40 | Temperature and moisture dependency of microbial growth | N2O,SOC |
| METRX_F_MIC_M_WEIBULL_1 | 0.6 | 0.3 | 0.7 | Temperature and moisture dependency of microbial growth | SOC |
| METRX_F_MIC_M_WEIBULL_2 | 9 | 5 | 20 | Temperature and moisture dependency of microbial growth | SOC |
| name | mean | min | max | coderef | calibration_target |
|---|---|---|---|---|---|
| METRX_AMAX | 1 | 0.5 | 1.5 | Microbial dynamics | N2O,SOC |
| METRX_F_MIC_T_EXP_1 | 3.5 | 2 | 5 | Temperature and moisture dependency of microbial growth | N2O,SOC |
| METRX_F_MIC_T_EXP_2 | 35 | 25 | 40 | Temperature and moisture dependency of microbial growth | N2O,SOC |
| METRX_MUEMAX_C_DENIT | 0.5 | 0.2 | 2 | Denitrifier growth | N2O |
| METRX_KMM_C_DENIT | 0.005 | 0.0001 | 0.01 | Denitrifier growth | N2O |
| METRX_KMM_N_DENIT | 0.002 | 0.0001 | 0.01 | Denitrifier growth | N2O |
| METRX_F_DENIT_M_WEIBULL_1 | 0.85 | 0.4 | 0.95 | Temperature and moisture dependency of denitrifier growth | N2O |
| METRX_F_DENIT_M_WEIBULL_2 | 25 | 6 | 30 | Temperature and moisture dependency of denitrifier growth | N2O |
| METRX_F_DENIT_NO | 14 | 8 | 20 | Denitrifier nitrogen use | N2O |
| METRX_F_DENIT_N2_1 | 0.7 | 0.2 | 1 | Denitrifier nitrogen use | N2O |
| METRX_F_DENIT_N2_2 | 0.85 | 0.15 | 0.9 | Denitrifier nitrogen use | N2O |
| METRX_F_DENIT_PH_1 | 4.3 | 3 | 5.5 | Denitrifier growth | N2O |
| METRX_F_DENIT_PH_2 | 0.9 | 0.3 | 1.5 | Denitrifier growth | N2O |
| METRX_F_DENIT_N2O_PH_1 | 5 | 3 | 5.5 | Denitrifier growth | N2O |
| METRX_F_DENIT_N2O_PH_2 | 0.6 | 0.3 | 1.5 | Denitrifier growth | N2O |
| METRX_F_NIT_FRAC_MIC | 0.35 | 0.1 | 1 | NH4 nitrification | N2O |
| METRX_F_NIT_NO_N2O_T_EXP_1 | 0.033 | 0.01 | 0.1 | Production of NO and N2O during nitrification | N2O |
| METRX_F_NIT_NO_N2O_T_EXP_2 | 8.9 | 7 | 15 | Production of NO and N2O during nitrification | N2O |
| METRX_F_NIT_NO_N2O_M_WEIBULL_1 | 0.7 | 0.1 | 0.9 | Production of NO and N2O during nitrification | N2O |
| METRX_F_NIT_NO_N2O_M_WEIBULL_2 | 10 | 4 | 15 | Production of NO and N2O during nitrification | N2O |
| METRX_F_NIT_NO_M_EXP_1 | 8 | 3 | 15 | Production of NO and N2O during nitrification | N2O |
| METRX_F_NIT_NO_M_EXP_2 | 0.3 | 0 | 1 | Production of NO and N2O during nitrification | N2O |
| METRX_KMM_O2_NIT | 0.01 | 0.001 | 0.1 | NH4 nitrification | N2O |
| METRX_KMM_NH4_NIT | 0.001 | 0.0001 | 0.01 | NH4 nitrification | N2O |
| METRX_KMM_NO2_NIT | 5e-05 | 1e-05 | 0.001 | NO2 nitrification | N2O |
| METRX_KF_NIT_NO_N2O | 0.007 | 0.001 | 0.1 | Production of NO and N2O during nitrification | N2O |
| METRX_F_SANVF_1 | 2 | 1.6 | 3.5 | Anaerobic volume | N2O,NO |
| METRX_F_SANVF_2 | 7 | 6.3 | 20 | Anaerobic volume | N2O,NO |
| METRX_D_EFF_EXP_AIR | 2.333 | 1 | 4 | Effective diffusion coefficient | O2,N2O,NO |
| name | mean | min | max | coderef | calibration_target |
|---|---|---|---|---|---|
| METRX_F_SANVF_1 | 2 | 1.6 | 3.5 | Anaerobic volume | N2O,NO |
| METRX_F_SANVF_2 | 7 | 6.3 | 20 | Anaerobic volume | N2O,NO |
| METRX_D_EFF_EXP_AIR | 2.333 | 1 | 4 | Effective diffusion coefficient | O2,N2O,NO |
Available model options: Default options are marked with bold letters.
yes for agricultural rice production ecosystems for which growth of algae should be considered.Surface bulk, e.g., water table (default: "surfacebulk" = yes / no) Automatically includes additional surface layers in case surface water table builds up.
Under construction.
MeTrx includes several model-specifc output options:
In order to include a MeTrx specific output, add the according attribute to the sinks section in the project file. Example:
The allocation of soil organic matter to various humus pools is primarily influenced by the C/N ratio within each pool, while adhering to the overall constraint of maintaining the soil's overarching C/N ratio.
The target C/N ratio of all mineral associated organic matter pools depend on the overall soil C/N ratio. Humus pool 1 representes non-protected organic matter. Humus pool 2 and 3 represent "old" and "very old" protected soil organic matter, respectively:
\begin{eqnarray*} C/N_{hum,1} &=& C/N_{soil} \\ C/N_{hum,2} &=& 1.5 \cdot C/N_{soil} \\ C/N_{hum,3} &=& METRX\_CN\_FRAC\_HUM3 \cdot C/N_{soil} \\ \end{eqnarray*}
Active organic material is assigned to microbial necromass (15%) and mineral associated but non-protected organic matter (humus pool 1: 85%).
Incoming litter from, e.g., plants, algae, animals is fragmentated to 'soil organic' litter (no more distinguishable from soil organic matter)
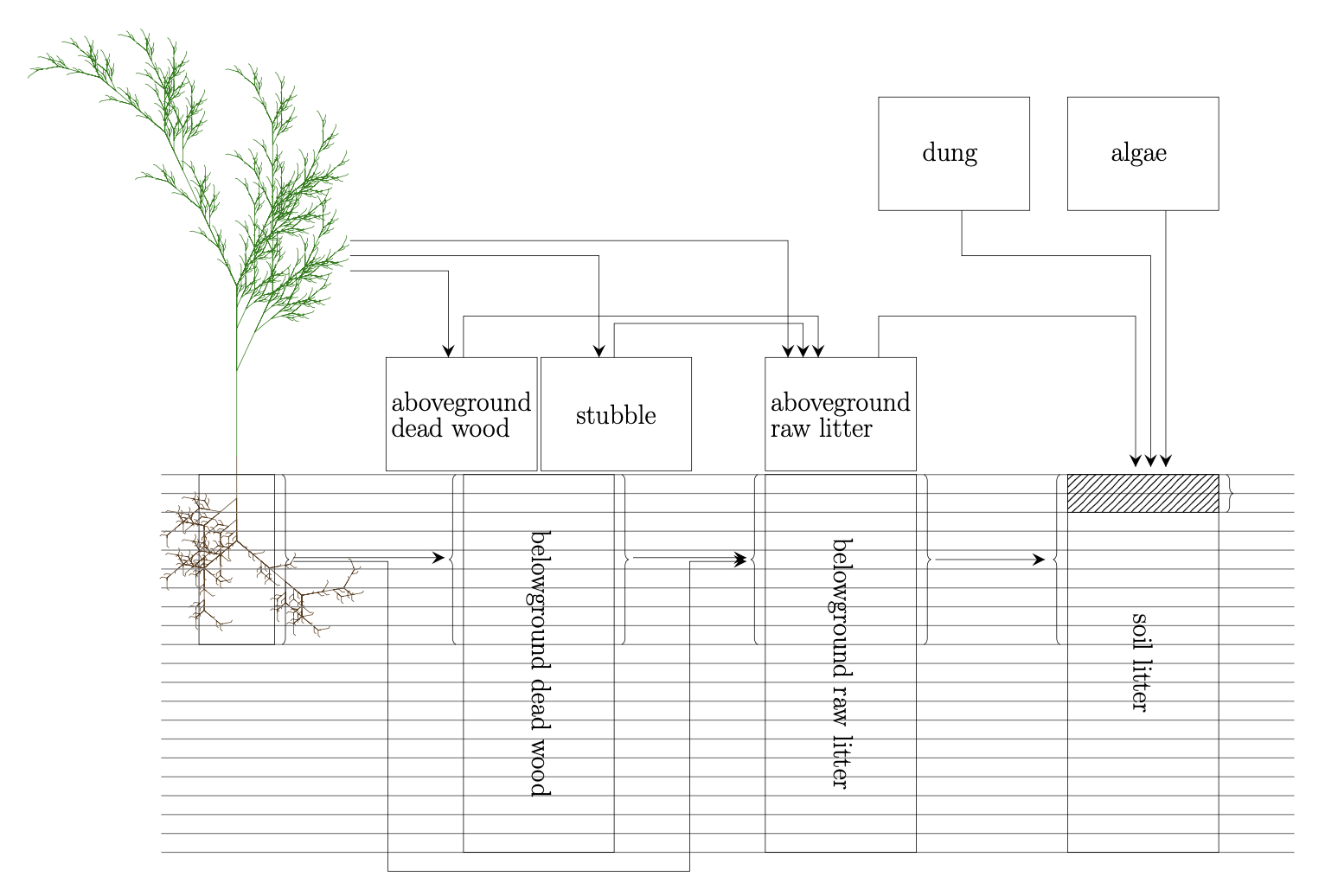
Turnover of soil organic matter (SOM) includes
Dissolved organic carbon is distinguished between the aerob and the anaerob soil and facilitates microbial metabolism (e.g., nitrification, denitrification, fermentation, ...). During fermentation and synthrophic metabolism, anaerob DOC can be further metabolized to acetate and molecular hydrogen, which serves methanogenic microbes as substrate. Decomposed nitrogen is always transferred to the dissolved organic nitrogen pool (DON) from where it is subsequently redistributed depending on pool specific target CN ratios.
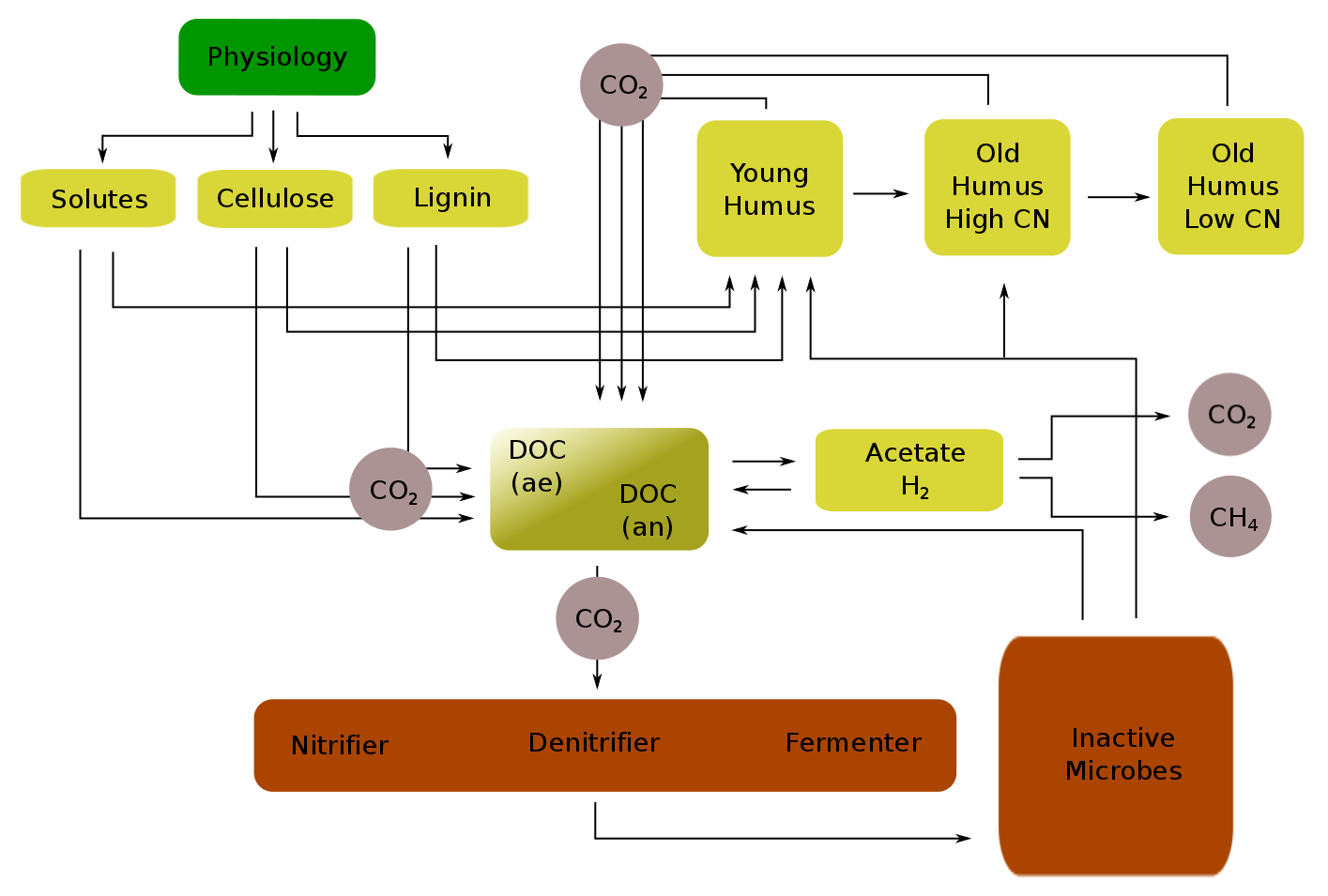
Turnover of microbial necromass involves:
Decomposition of inactive microbial carbon \( m_{imc} \) and nitrogen \( m_{imn} \) depends on soil temperature, soil moisture and soil anaerobicity:
\begin{eqnarray*} \Delta m_{imc \rightarrow doc_{ae}} = K\_DC\_AORG \cdot m_{imc} \cdot \phi_{tm} \cdot \phi_{till} \cdot (1 - anvf) \\ \Delta m_{imc \rightarrow doc_{an}} = K\_DC\_AORG \cdot m_{imc} \cdot \phi_{tm} \cdot \phi_{till} \cdot anvf \\ \Delta m_{imn} = \frac{\Delta m_{imc \rightarrow doc_{ae}} + \Delta m_{imc \rightarrow doc_{ae}}}{CN_{im}} \\ \end{eqnarray*}
Temperature moisture factor
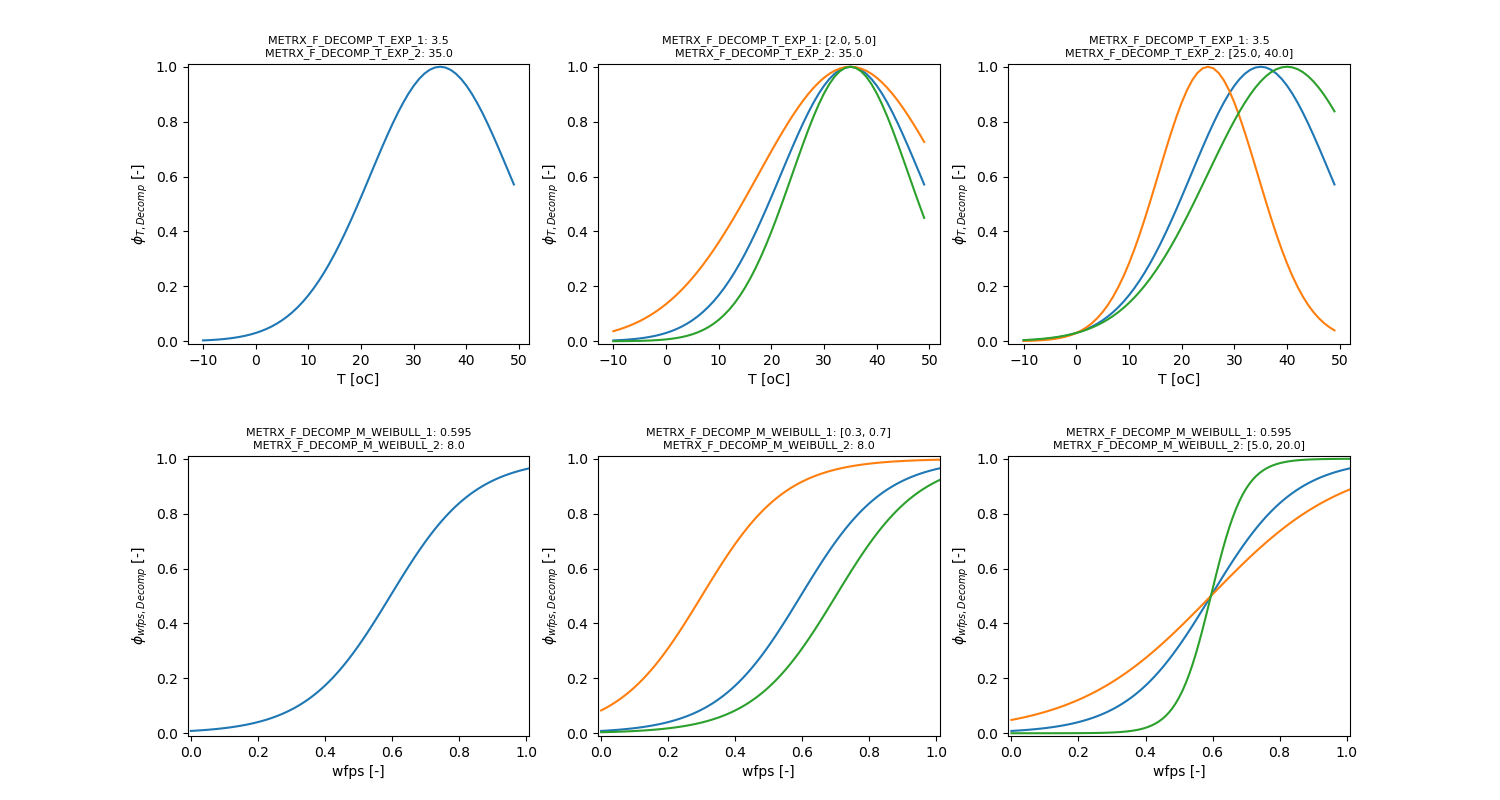
\begin{eqnarray*} \Delta m_{imc \rightarrow hum (young)} = METRX\_KR\_HU\_AORG\_HUM\_0 \cdot m_{imc} \\ \Delta m_{imc \rightarrow hum (old, high CN)} = METRX\_KR\_HU\_AORG\_HUM\_1 \cdot m_{imc} \\ \end{eqnarray*}
Turnover of SOM and plant debris includes:
Turnover rates depend on:
Depending on the litter or humus pool the general turnover rate is given by:
\[ \frac{dm_x}{dt} = K_x \cdot m_x \cdot \Pi_i \phi_{i} \]
with \( \Pi_i \phi_{i} \) being the multiplicative combination of pool specific environmental reduction factors \( \phi_{i} \) (e.g., temperature, moisture,...) determining turnover.
The influence of temperature and moisture is given by:
\[ \phi_{t,m} = \frac{2}{\frac{1}{\phi_{t}} + \frac{1}{\phi_{m}}} \]

\[ \phi_{lig} = e^{-METRX\_BETA\_LITTER\_TYPE \cdot \frac{c_{lig}}{c_{tot}}} \]
The influence of litter quality (C/N ratio) is given by:
\[ \phi_{litter} = 1 - METRX\_KR\_REDUCTION\_CN \cdot \frac{C_{lit}}{N_{lit}} \]
The influence of C/N ratio on anaerobic decomposition of humus pool 2 / organic soil
\[ \phi_{cn,org. soil} = 1 - \frac{1}{1 + e^{-0.5 (C/N - 30}} \]
The influence of clay content is given by
\[ \phi_{clay} = METRX\_F\_DECOMP\_CLAY\_1 + (1- METRX\_F\_DECOMP\_CLAY\_1) \cdot e^{-METRX\_F\_DECOMP\_CLAY\_2 \cdot c_{clay}} \]
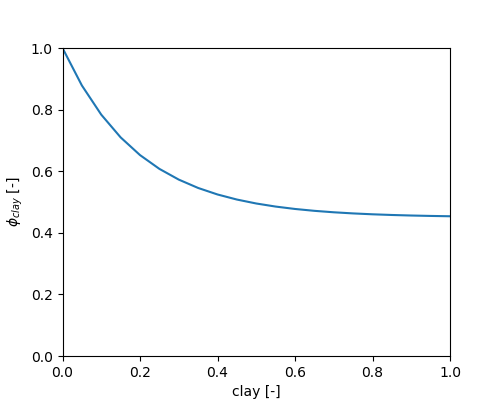
\begin{eqnarray*} \frac{dm_x}{dt} &=& \frac{dm_{x, anvf}}{dt} + \frac{dm_{x, aevf}}{dt} \\ \frac{dm_{x, anvf}}{dt} &=& K_x \cdot m_x \cdot \Pi_j \phi_{j} \cdot METRX\_KR\_REDUCTION\_ANVF \cdot anvf \\ \frac{dm_{x, aevf}}{dt} &=& K_x \cdot m_x \cdot \Pi_j \phi_{j} \cdot (1 - \end{eqnarray*}
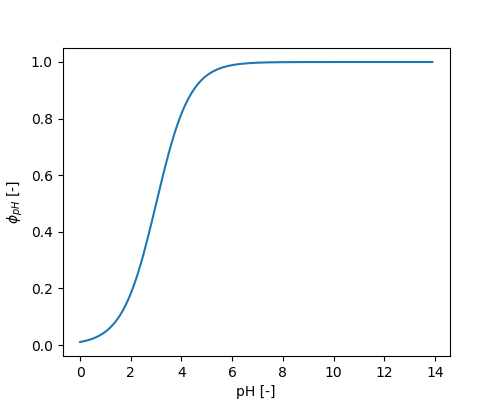
The influence of pH is given by:
\[ \phi_{pH} = \frac{1}{1 + e^{-METRX\_F\_DECOMP\_PH\_1 \cdot (pH - METRX\_F\_DECOMP\_PH\_2)}} \]
| Pool | Parameter | tilling | Temp. Moisture | pH | litter type | litter C/N | clay | O2 |
|---|---|---|---|---|---|---|---|---|
| Solutes | METRX_KR_DC_SOL | yes | yes | yes | yes | yes | no | yes |
| Cellulose | METRX_KR_DC_CEL | yes | yes | yes | yes | yes | no | yes |
| Lignin | METRX_KR_DC_CEL | yes | yes | yes | yes | yes | no | yes |
| Humus 1 | METRX_KR_DC_HUM1 | yes | yes | yes | no | no | yes | yes |
| Humus 2 | METRX_KR_DC_HUM2 | yes | yes | yes | no | no | yes | yes |
| Humus 3 | METRX_KR_DC_HUM3 | yes | yes | yes | no | no | yes | yes |
Decomposed carbon is added to DOC:
\begin{eqnarray*} \frac{dDOC_{ae}}{dt} &=& -\frac{dC_{x, aevf}}{dt} \\ \frac{dDOC_{an}}{dt} &=& -\frac{dC_{x, anvf}}{dt} \end{eqnarray*}
Decomposed nitrogen is partly mineralized and partly added to DON:
\begin{eqnarray*} \frac{dNH_4}{dt} &=& -0.5 \frac{dN_{x}}{dt} \\ \frac{dDON}{dt} &=& -0.5 \frac{dN_{x}}{dt} \end{eqnarray*}
Microbial growth is given by:
\[ \frac{c_{mic}}{dt} = c_{mic} \mu_{mic} \phi_{tm} \phi_{DOC} \]
Microbial activity \( \phi_{tm} \) is given a harmonic mean of a soil temperature ( \( \phi_{t}\)) and a soil water ( \( \phi_{m}\)) depending response coefficient.
\[ \phi_{tm} = \frac{\phi_{t} + \phi_{m}}{\frac{1}{\phi_{t}} + \frac{1}{\phi_{m}}} \]
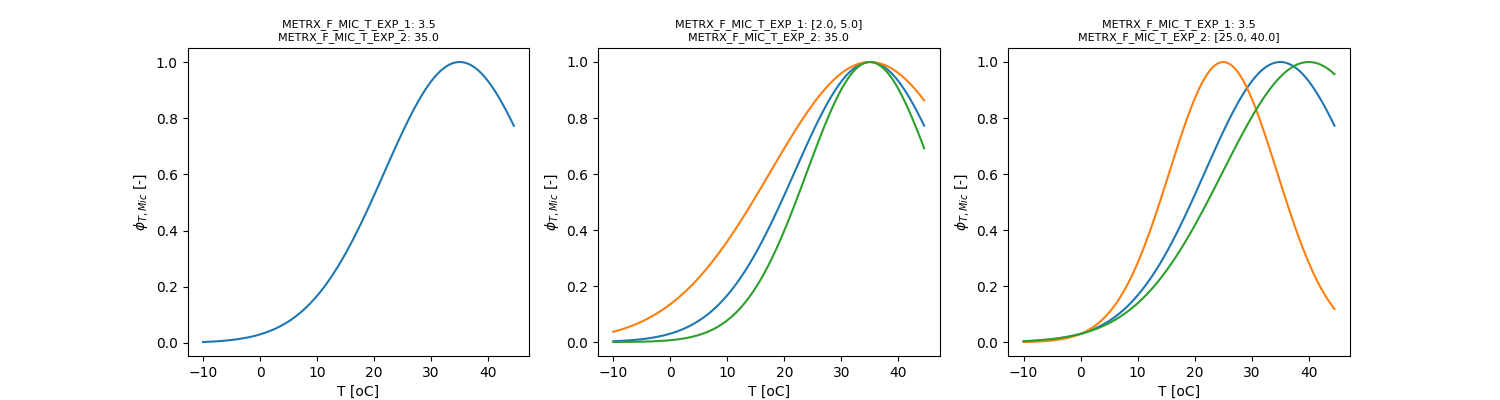
with \( \phi_{t}\) given by:
\[ \phi_{t} = e^{-\Omega_{MFMTE1} \cdot \left( 1 - \frac{T}{\Omega_{MFMTE2}} \right)^2} \]
\[ \phi_{m} = 1 - \frac{1}{1 + e^{(wfps - \Omega_{MFMMW1}) \cdot \Omega_{MFMMW2}}} \]
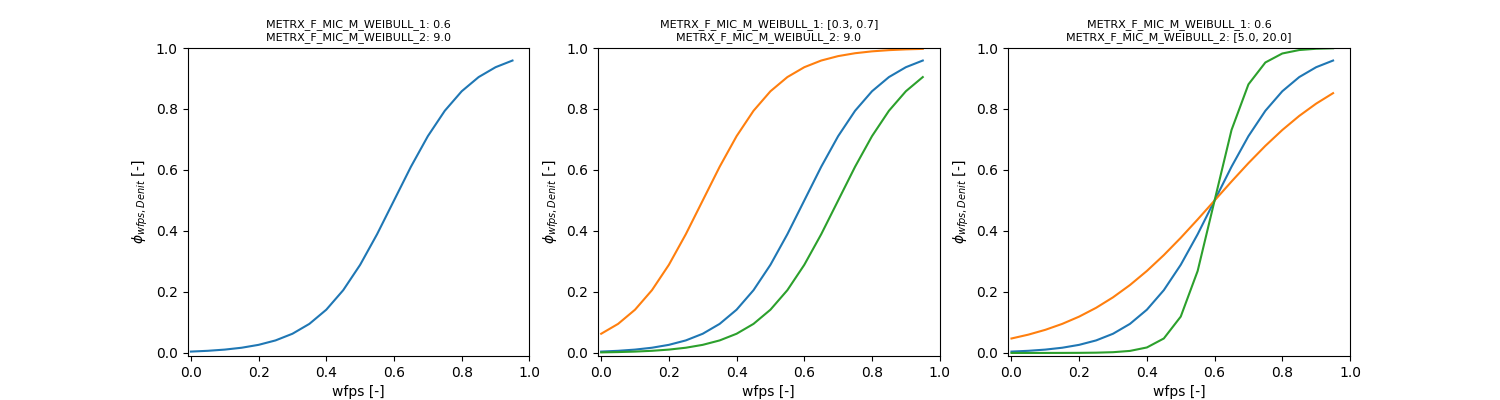
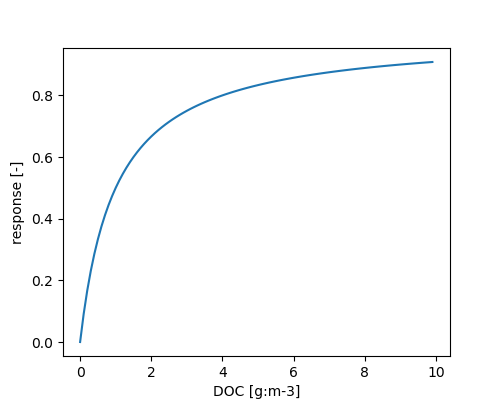
The dependency of microbial growth on DOC is given by:
\[ \phi_{DOC} = \frac{DOC}{DOC + \Omega_{MKCM}} \]
Microbial loss of biomass via maintenance respiration \( \frac{c_{mic,r}}{dt} \) and death \( \frac{c_{mic,d}}{dt} \) are calculated after [7] :
\begin{eqnarray*} \frac{c_{mic,r}}{dt} &=& c_{mic} a_{mic} \phi_{tm} (1 - Y_r) \\ \frac{c_{mic,d}}{dt} &=& c_{mic} a_{mic} \phi_{tm} \phi_{C} \end{eqnarray*}
\( \phi_{tm}: \) Microbial activity
\[ \phi_{C} = \frac{1}{1 + \Omega_{MKCM} \cdot DOC} \]
Nitrification is modeled as a two-stage process:
\[ NH_4^+ \rightarrow NO_2^- \rightarrow NO_3^- \]
depending on microbial biomass.
The first step of Nitrification is given by:
\[ \frac{d NH_4^+}{dt} = -c_{mic} a_{mic} \mu_{mic} \phi_{NH_4^+} \phi_{O_2} \phi_{ph} \phi_{ni} \]
\( c_{mic}: \) Microbial biomass
\( a_{mic}: \) Microbial activity
\( \mu_{mic}: \) Microbial growth rate
\( \phi_{NH_4^+}: \) Microbial growth dependency on DOC
\( \phi_{O_2}: \) Microbial growth dependency on O2
\( \phi_{ph}: \) Microbial growth dependency on NH4
\( \phi_{ni}: \) Effect of nitrification inhibitor
The activity coefficient of nitrifier \( a_{mic} \) is given by a harmonic mean of a soil temperature ( \( \phi_{T}\)) and a soil water ( \( \phi_{wfps}\)) depending response coefficient.
\[ a_{mic} = \frac{\phi_{T} + \phi_{wfps}}{\frac{1}{\phi_{T}} + \frac{1}{\phi_{wfps}}} \]
with \( \phi_{T}\) given by:
\[ \phi_{T} = e^{-METRX\_F\_MIC\_T\_EXP\_1 \cdot \left( \frac{1 - T}{METRX\_F\_MIC\_T\_EXP\_2} \right)^2} \]

\[ \phi_{wfps} = 1 - \frac{1}{1 + e^{(wfps - METRX\_F\_MIC\_M\_WEIBULL\_1) \cdot METRX\_F\_MIC\_M\_WEIBULL\_2}} \]

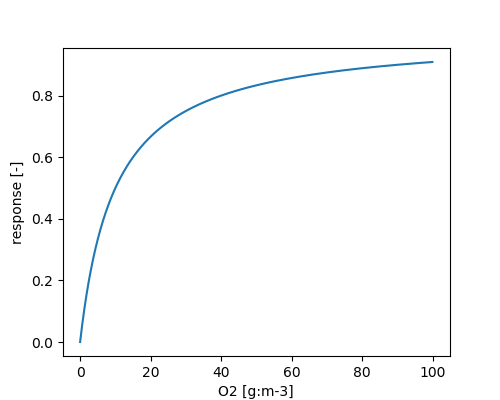
\[ \phi_{NH_4^+} = \frac{NH_4^+}{NH_4^+ + METRX\_KMM\_NH4\_NIT} \]
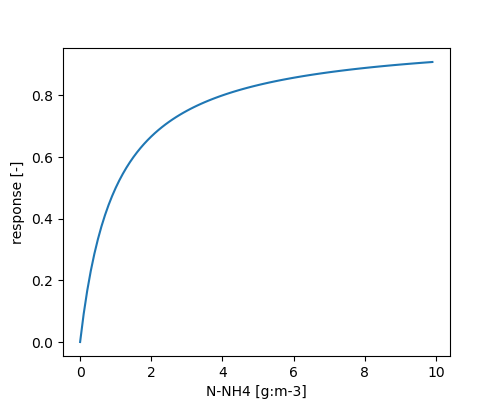
\[ \phi_{O_2} = \frac{O_2}{O_2 + METRX\_KMM\_O2\_NIT} \]
The influence of nitrification inhibitor is given by Enhanced efficiency nitrogen fertilizers.
During the first step of nitrification a certain amount of N ist lost in form of \( NO \) and \( N_2O \). The relevant processes are a mix of:
Reported production of \( NO \) during nitrification:
All \( N_2O \) produced in connection with nitrification was initially \( NO \). Emissions of \( NO \) and \( N_2O \) during nitrification are likely influenced by soil temperature and moisture (Chen et al. 2010):
\[ \frac{d (NO+N_2O)}{dt} = - \Omega_{MKNNN} \cdot \frac{d NH_4^+}{dt} \phi_{NO+N2O, T, wfps} \]
The associated factor \( \phi_{NO+N2O, T, wfps} \) is given by a harmonic mean of a soil temperature ( \( \phi_{NO+N2O, T} \)) and a soil water ( \( \phi_{NO+N2O, wfps} \)) depending response coefficient:
\[ \phi_{NO+N2O, T, wfps} = \frac{2.0}{\frac{1.0}{\phi_{NO+N2O, T}} + \frac{1.0}{\phi_{NO+N2O, wfps}}} \]
with \( \phi_{NO+N2O, T}\) given by:
\[ \phi_{NO+N2O, T} = \Omega_{MFNNNTE1} \cdot e^{\frac{T}{\Omega_{MFNNNTE2}}} \]
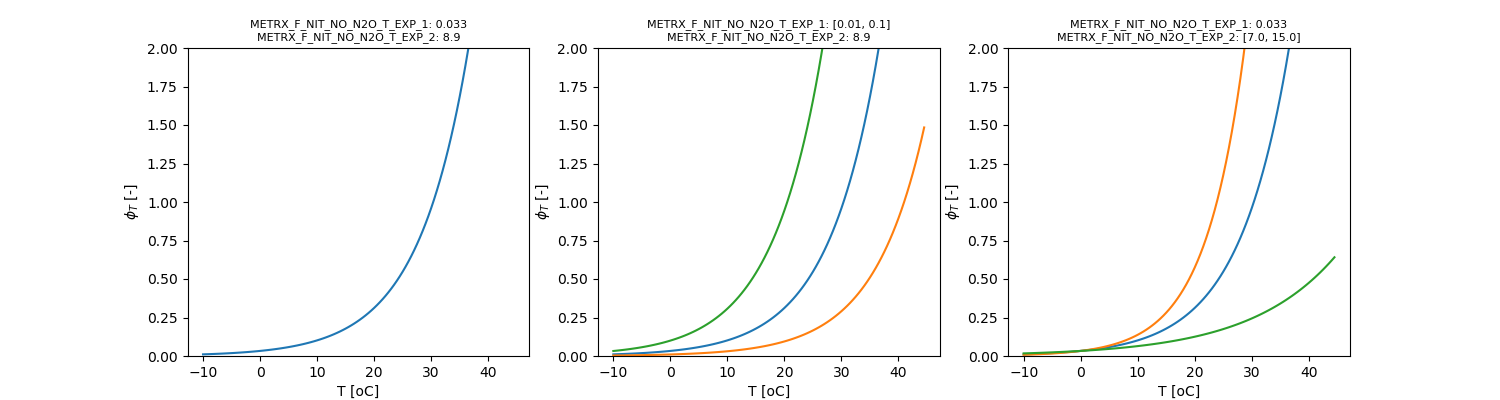
\[ \phi_{NO+N2O, wfps} = 1 - \frac{1}{1 + e^{(wfps - \Omega_{MFNNNMW1}) \cdot \Omega_{MFNNNMW2}}} \]
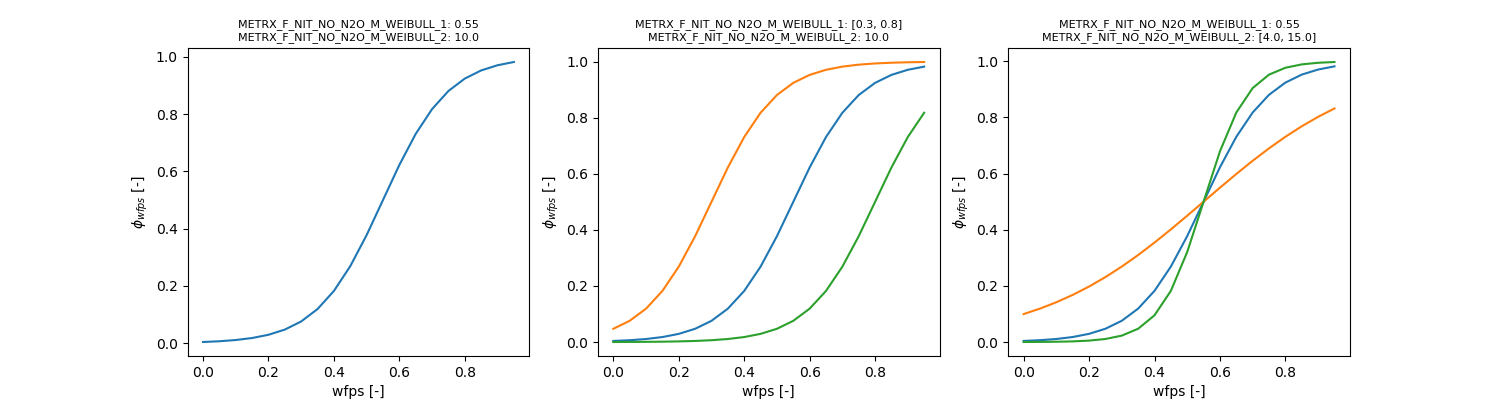
\[ \frac{d (NO)}{dt} = \frac{d (NO+N_2O)}{dt} \cdot \phi_{NO, wfps} \]
with
\[ \phi_{NO, wfps} = 1 - \frac{1}{ 1 + e^{-\Omega_{MFNNME1} \cdot (wfps - \Omega_{MFNNME2})}} \]
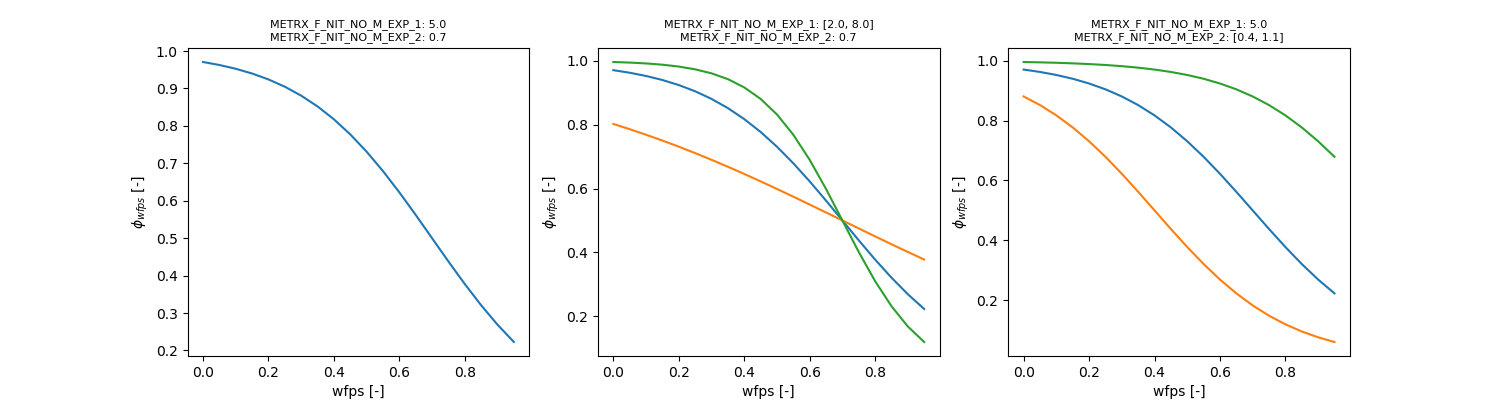
The second step of nitrification is calculated independent of microbial biomass:
\[ \frac{d NO_2^-}{dt} = \frac{NO_2^-}{METRX\_KMM\_NO2\_NIT + NO_2^-} \]
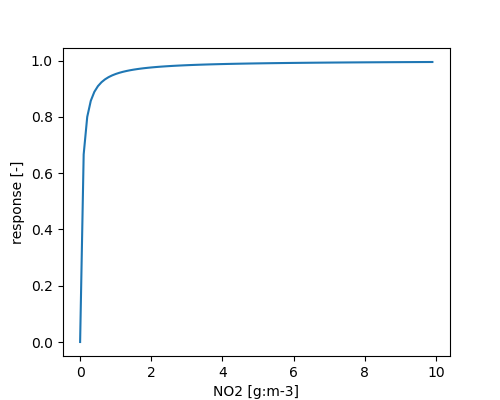
Denitrification is calculated as four-step process including the nitrogen species \( NO_3^-, NO_2^-, NO \) and \( N_2O \):
\[ NO_3^- \rightarrow NO_2^- \rightarrow NO \rightarrow N_2O \rightarrow N_2 \]
All denitrification steps are calculated based on actively denitrifying microbial biomass. The associated activity coefficient of denitrifying microbes \( a_{mic} \) is given by temperature and moisture dependency.
The temperature and moisture dependency of denitrifying microbes is given by the harmonic mean of a soil temperature ( \( \phi_{T}\)) and a soil moisture ( \( \phi_{wfps}\)) response coefficient.
\[ \frac{2}{\frac{1}{\phi_{T}} + \frac{1}{\phi_{wfps}}} \]
The soil temperature response \( \phi_{T}\) of denitrification is given by the same temperature dependency as for general microbial activity:
\[ \phi_{T} = e^{-\Omega_{MFMTE1} \cdot \left( 1 - \frac{T}{\Omega_{MFMTE2}} \right)^2} \]
.

\[ \phi_{wfps} = 1 - \frac{1}{1 + e^{(wfps - \Omega_{MFDMW1}) \cdot \Omega_{MFDMW2}}} \]
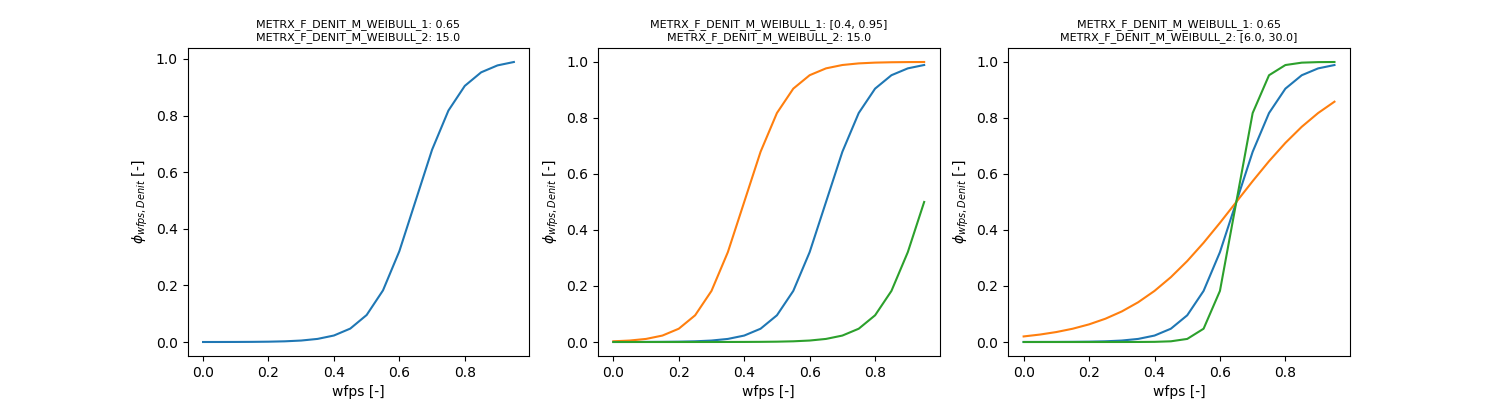
\begin{eqnarray*} \phi_{C} &=& \frac{DOC}{DOC + METRX\_KMM\_C\_DENIT} \\ \phi_{N} &=& \frac{N_{total}}{N_{total} + METRX\_KMM\_N\_DENIT} \\ \phi_{C,N} &=& \frac{2}{\frac{1}{\phi_{C}} + \frac{1}{\phi_{N}}} \end{eqnarray*}
Microbial enzymes relevant for denitrification are:
Heterotrophic denitrification decreases with increasing pH (Kool et al. 2010). Low pH inhibits all enzymes but especially nosZ. The general pH influence on microbial denitrifier growth influencing all enzymes is given by:
\[ \phi_{pH} = 1 - \frac{1}{1 + e^{\frac{ph - METRX\_F\_DENIT\_PH\_1}{METRX\_F\_DENIT\_PH\_2}}} \]
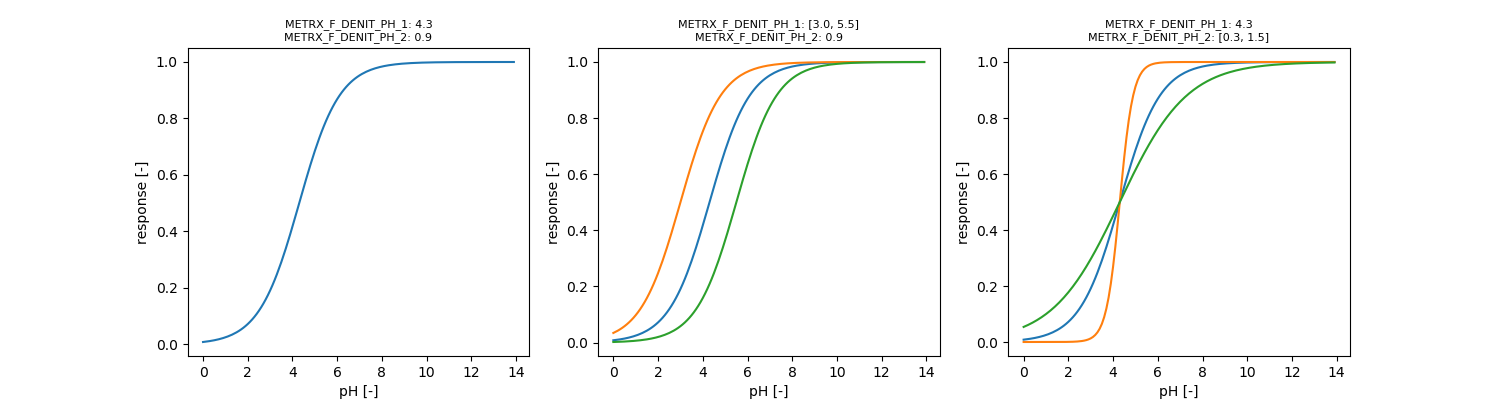
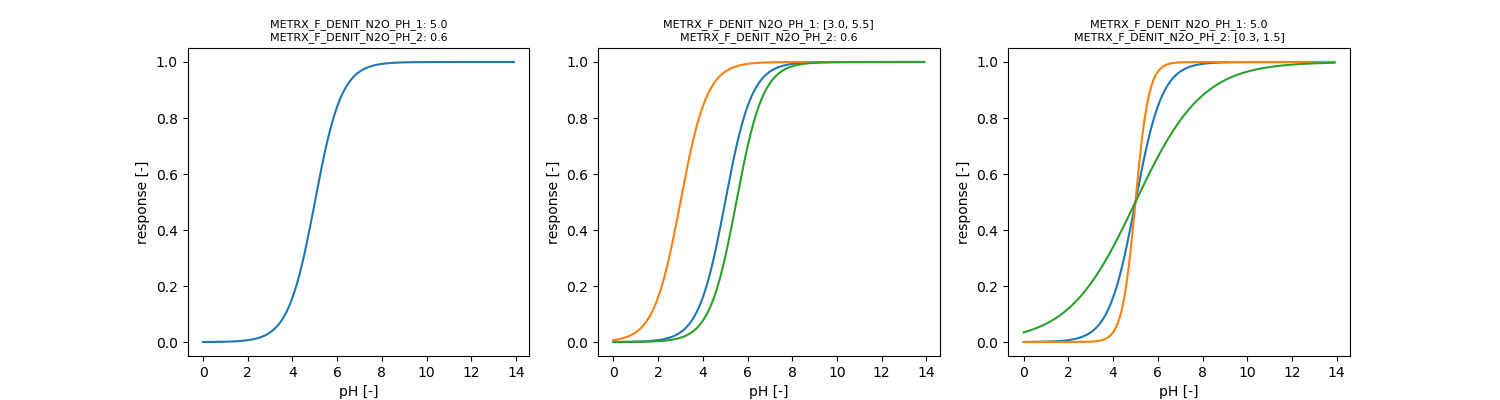
\[ \phi_{pH,nosZ} = 1 - \frac{1}{1 + e^{\frac{ph - METRX\_F\_DENIT\_N2O\_PH\_1}{METRX\_F\_DENIT\_N2O\_PH\_2}}} \]
\begin{eqnarray*} C_{demand} &=& c_{mic} \mu_{mic} a_{mic} \frac{1.0}{Y_{denit}} \phi_{C,N} \phi_{pH} \\ C_{demand, assi} &=& C_{demand} Y_{denit} \\ C_{demand, diss} &=& C_{demand} (1 - Y_{denit}) \end{eqnarray*}
The denitrification efficiency is constant:
\[ Y_{denit} = METRX\_MIC\_EFF\_ANAEROBIC\_RESPIRATION \]
Denitrification of \( N_x \) depends on their relative abundance using associated scaling factors:
\begin{eqnarray*} \psi_{NO_3^-} &=& \frac{NO_3^-}{NO_3^- + NO_2^- + NO + N_2O} \\ \psi_{NO_2^-} &=& (1- \psi_{NO_3^-}) \cdot \frac{NO_2^-}{NO_2^- + NO + N_2O} \\ \psi_{NO} &=& (1- \psi_{NO_3^-}) \cdot \frac{NO}{NO_2^- + NO + N_2O} \\ \psi_{N_2O} &=& (1- \psi_{NO_3^-}) \cdot \frac{N_2O}{NO_2^- + NO + N_2O} \\ \end{eqnarray*}
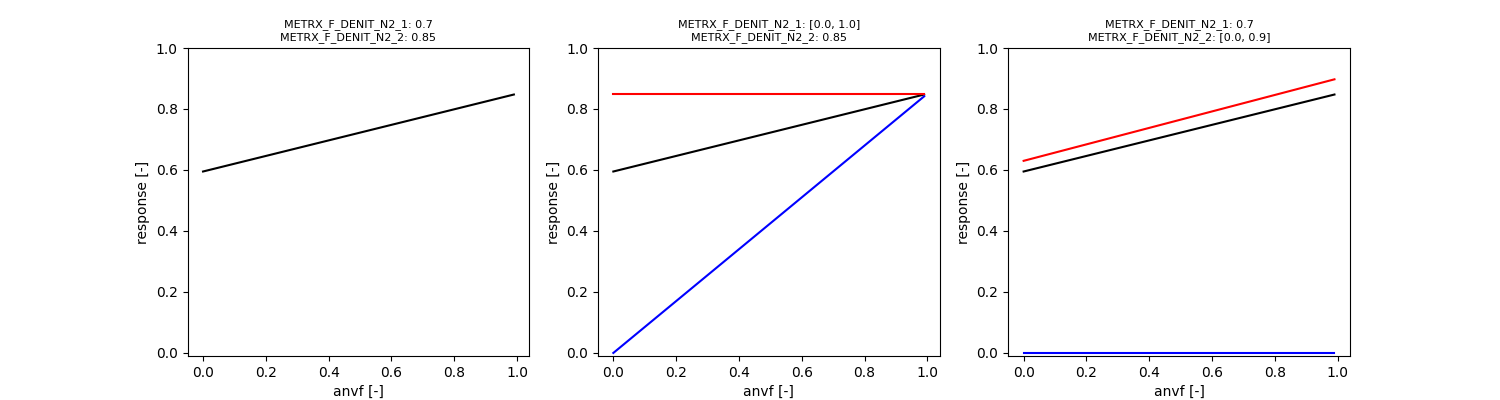
\( N_x \) can be denitrified a sinlge step or multiple steps before it is released from the denitrifying microbial organism to the soil environment. The fraction of \( N_x \), which is completely denitrified to \( N_2 \) within the same organism depends on the soil anaerobic volume (assuming denitrification enzymes are more developped under anaerobic conditions):
\[ \phi_{anvf,1} = \Omega_{MFDN1} \cdot \Omega_{MFDN2} + V_{an} \cdot (\Omega_{MFDN2} - \Omega_{MFDN1} \cdot \Omega_{MFDN2}) \]
Currently, it is assumed that after denitrification of \( NO_3^- \), \( NO_2^- \) is always released to the environment:
\begin{eqnarray*} \frac{d NO_3^-}{dt} &=& \psi_{NO_3^-} \cdot C_{demand} \cdot \Xi_{CN, NO_3^-} \\ \Xi_{CN, NO_3^-} &=& \xi_{CN, NO_3^- \rightarrow NO_2^-} \\ \frac{d NO_3^-}{dt} &=& \frac{d NO_{3, \rightarrow NO_2^-}^-}{dt} \end{eqnarray*}
Denitrified \( NO_2^- \) is partly transferred to \( NO, N_2O \) and \( N_2 \) depending on the anaerobicity of the soil. The associated carbon demand is given by:
\begin{eqnarray*} \frac{d C_{NO_2^-}}{dt} &=& \psi_{NO_2^-} \frac{C_{denit}}{dt} \\ \frac{d C_{NO_2^- \rightarrow N_2}}{dt} &=& \frac{d C_{NO_2^-}}{dt} \cdot \phi_{anvf,1} \cdot \phi_{pH, nosZ} \\ \frac{d C_{NO_2^- \rightarrow NO}}{dt} &=& \frac{d C_{NO_2^-}}{dt} \cdot (1-\phi_{anvf,1}) \cdot \phi_{anvf,2} \\ \frac{d C_{NO_2^- \rightarrow N_2O}}{dt} &=& \frac{d C_{NO_2^-}}{dt} - \frac{d C_{NO_2^- \rightarrow N_2}}{dt} - \frac{d C_{NO_2^- \rightarrow NO}}{dt} \end{eqnarray*}
The stoichiometry between carbon and nitrogen is given by:
\begin{eqnarray*} \frac{d NO_{2, NO_2^- \rightarrow N_2}^-}{dt} &=& \xi_{CN, NO_2^- \rightarrow N_2} \frac{d C_{NO_2^- \rightarrow N_2}}{dt} \\ \frac{d NO_{2, NO_2^- \rightarrow NO}^-}{dt} &=& \xi_{CN, NO_2^- \rightarrow NO} \frac{d C_{NO_2^- \rightarrow NO}}{dt} \\ \frac{d NO_{2, NO_2^- \rightarrow N_2O}^-}{dt} &=& \xi_{CN, NO_2^- \rightarrow N_2O} \frac{d C_{NO_2^- \rightarrow N_2O}}{dt} \end{eqnarray*}
Denitrified \( NO \) is partly transferred to \( N_2O \) and \( N_2 \) depending on the anaerobicity of the soil. The associated carbon demand is given by:
\begin{eqnarray*} \frac{d C_{NO}}{dt} &=& \psi_{NO} \frac{C_{denit}}{dt} \\ \frac{d C_{NO \rightarrow N_2}}{dt} &=& \frac{d C_{NO}}{dt} \cdot \phi_{anvf,1} \cdot \phi_{pH, nosZ} \\ \frac{d C_{NO \rightarrow N_2O}}{dt} &=& \frac{d C_{NO}}{dt} - \frac{d C_{NO_2^- \rightarrow N_2}}{dt} \end{eqnarray*}
The stoichiometry between carbon and nitrogen is given by:
\begin{eqnarray*} \frac{d NO_{NO \rightarrow N_2}}{dt} &=& \xi_{CN, NO \rightarrow N_2} \frac{d C_{NO \rightarrow N_2}}{dt} \\ \frac{d NO_{NO \rightarrow N_2O}}{dt} &=& \xi_{CN, NO \rightarrow N_2O} \frac{d C_{NO \rightarrow N_2O}}{dt} \end{eqnarray*}
The associated carbon demand is given by:
\begin{eqnarray*} \frac{d C_{N_2O}}{dt} &=& \psi_{N_2O} \frac{C_{denit}}{dt} \\ \end{eqnarray*}
The stoichiometry between carbon and nitrogen is given by:
\begin{eqnarray*} \frac{d N_2O}{dt} &=& \xi_{CN, N_2O} \frac{d C_{N_2O}}{dt} \\ \end{eqnarray*}
At low pH (<4.5) \( N_2O \) can be produced via chemical decomposition of hydroxylamine (NH2OH), nitroxyl hydride (HNO) or \( NO_2^- \), which are intermediate products of ammonia oxidation (Zumft 1997; Wrageet al. 2001).
Temperature dependency of chemodenitrification:
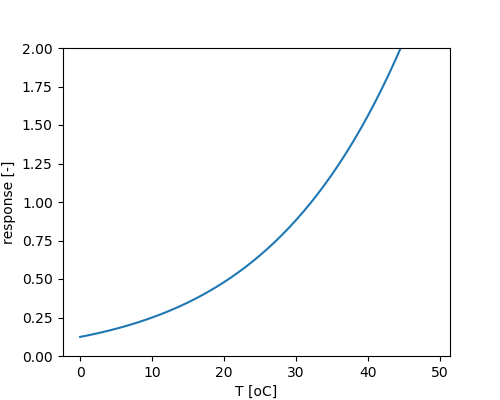
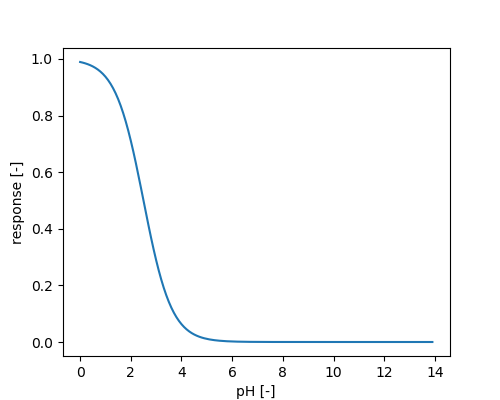
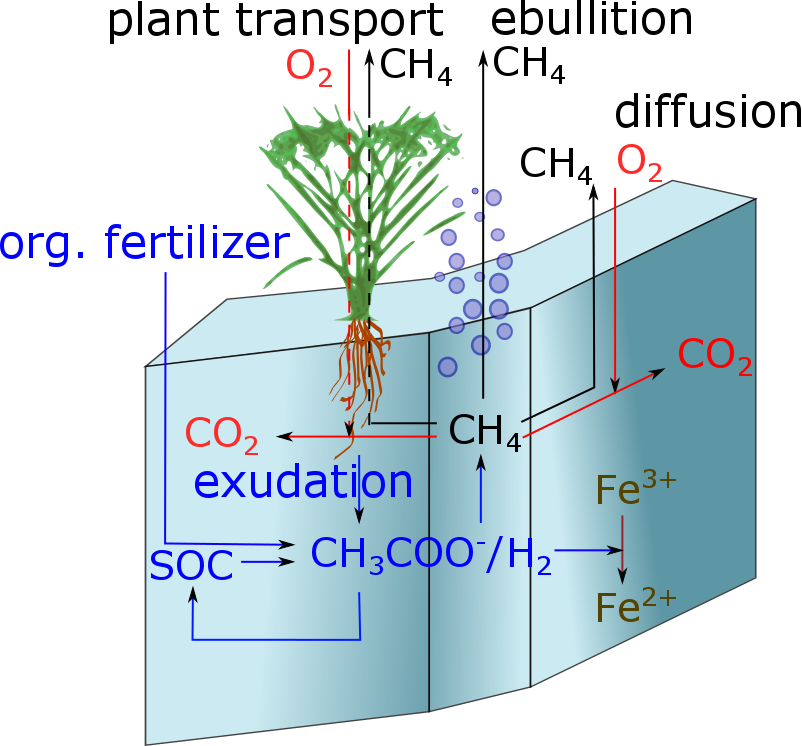
Under anaerobic conditions acetate and hydrogen are produced, which may serve as substrate for iron reducing and methanogenic bacteria.
Temperature dependency of microbial activity:
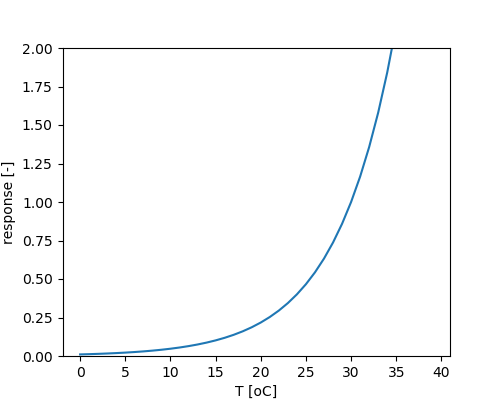
The stoecheometry of iron reduction via aceate is given by::
\[ CHCOO^- + 8 Fe^{3+} + 4 H_2O \rightarrow 2 HCO_3^- + 8 Fe^{2+} + 9 H^+ \]
The stoecheometry of iron reduction via aceate is given by::
\[ H_2 + 2 Fe^{3+} + 4 H^+ \rightarrow 2 Fe^{2+} + 6 H_2O \]
Iron reduction via acetate and hydrogen depends on the amount of Fe3+ and the amount of either aceatet or hydrogen each modeled using a Michaelis Menten kinetic. Further influencing factors are temperature, NO3 and O2:
\[ \frac{dFe^{3+}}{dt} = - METRX\_MUEMAX\_C\_FE\_RED \cdot \phi_{T} \cdot \phi_{NO3} \cdot \phi_{O2} \cdot \phi_{Fe3+} \cdot \phi_{AC/H2} \]
The dependy on NO3 is given by:
\[ \phi_{NO3} = 1 - \frac{NO3}{NO3 + NO3\_MOLAR\_MAX\_FE\_RED} \]
The stoecheometry of iron oxidation is given by::
\[ 4 Fe^{2+} + O_2 + 10 H_2O \rightarrow 4 Fe(OH)_3 + 8 H^+ \]
\[ \frac{dFe^{2+}}{dt} = - METRX\_KR\_OX\_FE \cdot Fe^{2+} \cdot \phi_{O2} \]
The dependy on O2 is given by:
\[ \phi_{O2} = \frac{O_2}{O_2 + METRX\_KMM\_O2\_FE\_OX} \]
\[ Fe^{3+} < METRX\_FRAC\_FE\_CH4\_PROD \cdot (Fe^{3+} + Fe^{2+}) \]
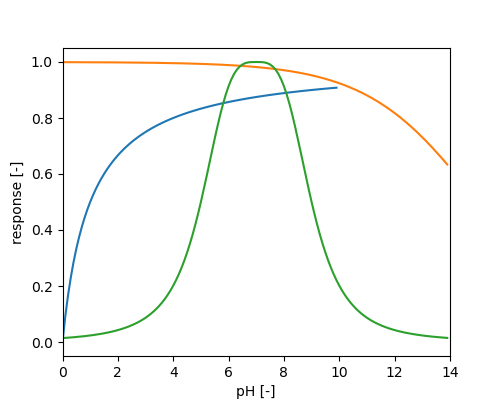
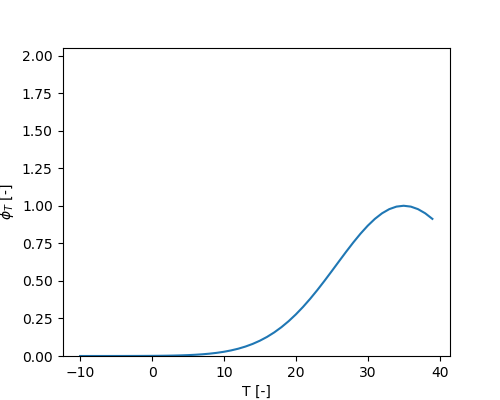
Methane production depends on temperature and pH:
\begin{eqnarray*} \phi_{T} &=& METRX\_F\_CH4\_PRODUCTION\_T\_EXP\_1 \\ && \left ( 1- \frac{1}{METRX\_F\_CH4\_PRODUCTION\_T\_EXP\_2} \right )^2 \\ \phi_{pH} &=& \frac{1}{1 + \left( \frac{|pH - 7|}{2} \right)^{3.4}} \\ \end{eqnarray*}
\[ CH_3COOH -> CO_2 + CH_4 \]
Acetoclastic methanogenesis is given by:
\[ \frac{d CH_4}{d t} = METRX\_MUEMAX\_C\_CH4\_PROD \cdot \phi_{CH_3COOH} \cdot \phi_T \cdot \phi_{pH} \cdot \phi_{O_2} \]
with \( \phi_{CH_3COOH}\) given by:
\[ \phi_{CH_3COOH} = \frac{CH_3COOH}{METRX\_KMM\_AC\_CH4\_PROD + CH_3COOH} \]
The stoecheometric formula for hydrogenotrophic methanogenesis is given by:
\[ 4 H_2 + CO_2 -> 2 H_2O + CH_4 \]
Hydrogenotrophic methanogenesis is given by:
\[ \frac{\partial CH_4}{\partial t} = METRX\_MUEMAX\_H2\_CH4\_PROD \cdot \phi_{H_2} \\ \cdot \phi_T \cdot \phi_{pH} \cdot \phi_{O_2} \]
The stoecheometry of methanotrophy is given by:
\[ CH_4 + (2-\alpha) O_2 \rightarrow (1-\alpha) CO_2 + (2-\alpha) H_2O + \alpha CH_2O \]
Methane oxidation depends on nitrogen, oxygen and methane concentration as well as temperature:
\begin{eqnarray*} \phi_{N} &=& (1- METRX\_F\_N\_CH4\_OXIDATION) \\ && METRX\_F\_N\_CH4\_OXIDATION \frac{N}{METRX\_KMM\_N\_CH4\_OX + N}\\ \phi_{O_2} &=& \frac{O_2}{METRX\_K\_O2\_CH4\_OX \cdot O_2} \\ \phi_{CH_4} &=& \frac{CH_4}{METRX\_KMM\_CH4\_CH4\_OX + CH_4} \\ \phi_{T} &=& METRX\_F\_CH4\_OXIDATION\_T\_EXP\_1 \\ && \left ( 1- \frac{1}{METRX\_F\_CH4\_OXIDATION\_T\_EXP\_2} \right )^2 \\ \end{eqnarray*}
\[ \frac{d CH_4}{d t} = - METRX\_MUEMAX\_C\_CH4\_OX \cdot \phi_{N} \cdot \phi_{O_2} \cdot \phi_{CH_4} \cdot \phi_{T} \]
Algae growth is only considered if option "algae" is set true.
Algae growth only takes place if ponding water table exists and incoming shortwave radiation directly above soil (below canopy) is greater zero.
Algae growth rate depends on:
\[ \phi_N = (1.0 - \Phi_{METRX\_F\_N\_ALGAE}) + \Phi_{METRX\_F\_N\_ALGAE} \cdot \frac{N}{\Phi_{METRX\_KMM\_N\_ALGAE} + N } \]
\[ \phi_T = \left\{ \begin{array}{cccc} 0.0 & T \le 15.0 \\ \frac{T - 15.0}{15.0} & 15.0 < T \le 30.0 \\ 1.0 - \frac{T - 30.0}{15.0} & 30.0 < T \le 45.0 \\ 0.0 & 45.0 > T \end{array} \right. \label{eq2} \]
\[ \phi_P = 1.0 - e^{\frac{-P}{100.0}} \]
Algae growth rate is given by:
\[ \mu_g = \Phi_{METRX\_MUEMAX\_C\_ALGAE} \cdot min(\phi_N, \phi_T, \phi_P) \]
Algae growth changes pH value of the ponding water table:
\[ \Delta pH = 3.0 \cdot \phi_N \cdot \phi_T \cdot \phi_P \]
Algae turnover:
\[ \mu_d = m_A \cdot \Phi_{METRX\_AMAX\_ALGAE} \]
The chemical equilibrium between dissolved \( NH_3 \) and \( NH_4 \) is given by (Sadeghi et al., 1988):
\begin{eqnarray*} f_{NH_3} &=& \frac{c_{NH_3}}{c_{NH_3} + c_{NH_4}} \\ f_{NH_3} &=& \frac{1}{1 + \frac{10^{-pH}}{K_a}} \\ K_a &=& 10^{\frac{-2728.3}{T} - 0.094219} \end{eqnarray*}
The chemical equilibrium between dissolved \( NH_3 \) and \( NH_4 \) is calculated for the surface water table and the soil solution.
Ammonium is partly adsorped at the soil surface depending on soil texture.
The effective diffusion coefficient \( D_{eff} \) relates to the tortuosity of the soil matrix. Two different approaches can be chosen (see also Model options):
\[ D_{eff} = \theta_{g}^{\Omega_{MDEEA}} \]
\[ D_{eff} = \frac{\theta_{g}^{10/3}}{\theta_{p}^2} \]
Radon (Ra-222) is created via the decay chain of U-238, with Ra-226 as the immediate parent material. It has a half-life of 3.8 days, and during this time can diffuse through the soil and be emitted into the atmosphere. Radon concentration is typically measured in the units Bqm$^{-3}$ - i.e. the number of radon decays per second per cubic metre. LDNDC thus uses the unit Bqm$^{-2}$ for the 'mass' per square metre of Ra-222 in a soil layer. While Bq is a measure of decays per second rathern than mass, it is simple to convert between the two. True mass (kg) can be determined by multiplying by the atomic mass of Ra-222 divided by the Ra-222 decay constant.
Phase equilibrium betwenn dissolved and gaseous state is calculated throughout the soil profile as well as for the top layer of the surface water table (if existing).
For the following species the phase equilibrium betwenn dissolved and gaseousstate is calculated:
For the equilibrium between the partial pressure in the gas pahse \( p_{i,gas} \) and the concentrations in the dissolved species \( i \), the Henry law is applied:
\[ c_{i,liq} = H_{i} p_{i,gas} \]
Gaseous diffusion is calculated for:
For the bottom, a Neuman no-flow boundary condition is used and for the top a Dirichlet boundary condition is used.
Diffusion of dissolved species is calculated for:
The amount of dissolved matter that leaves the simulated domain is added to the leaching output.
If there is a calculated inflow of matter, there is a following correction of mass. The mass is scaled down throughout the whole profile by the amount of calculated mass inflow.
Ebullition is calculated in the soil as well as in the water table. Considered substances are CH4, CO2, O2, NH3, NO, N2O and N2.
Gas bubbles can be fomred as soon as a critical water filled pore space is reached.
Ebullition occurs as soon as total pressure (CH4 + CO2 + ...) exceeds static pressure. Once formed, gas bubbles are transported upwards not being dissolved in upper soil layers as long as water filled pore space is below critical water filled pore space.
If water filled pore space is below critical water filled pore space, gas bubbles are dissolved.
MeTrx considers for a subset of carbon and nitrogen species a horizontal (within one soil layer) differentiation between aerobic and anaerobic parts of the soil. The differentiation is based on the oxygen partial pressure, which in turn is mainly determined by the water profile, respiration processes and gaseous diffusion of oxygen.
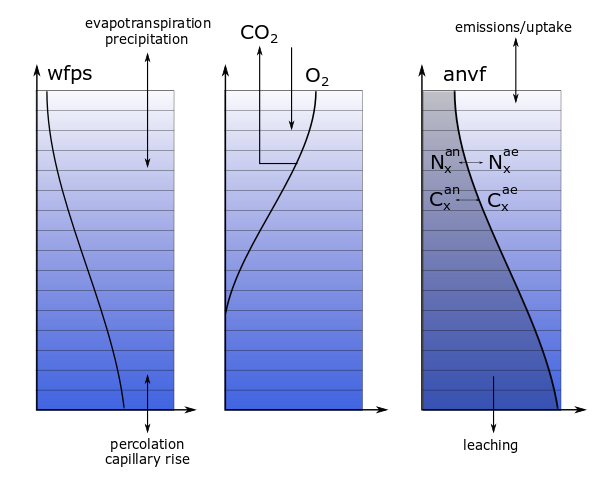
Two anaerobic volumes \( V_{an,x} \) are distinguished, both depending on the oxygen partial pressure \( p_{O_2} \) in bar:
\[ V_{an,r} = e^{-(\Omega_{MFR2} \cdot p_{O_2})^{\Omega_{MFR1}}} \]
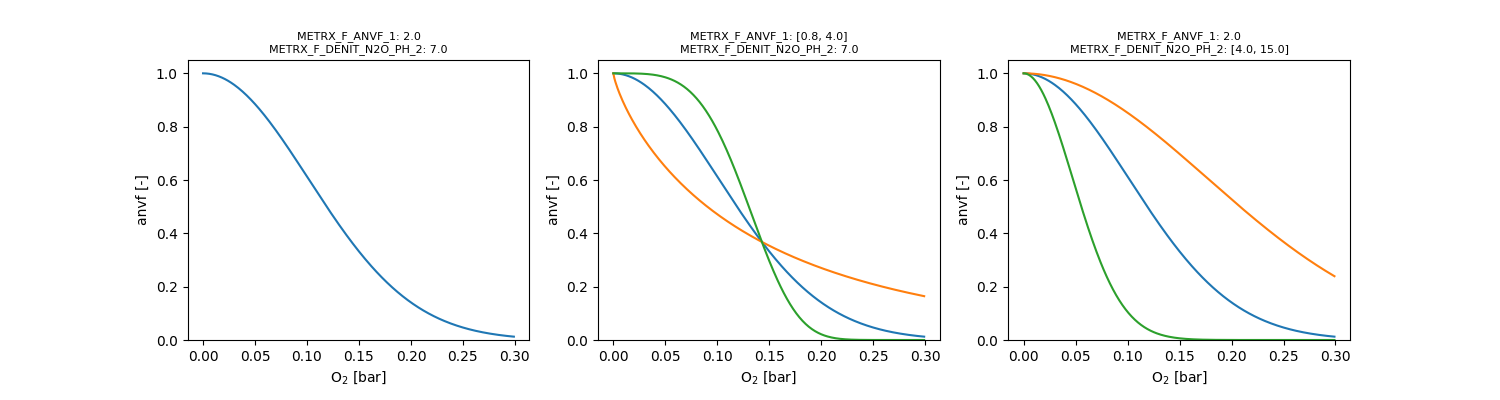
\[ V_{an,s} = e^{-(\Omega_{MFS2} \cdot p_{O_2})^{\Omega_{MFS1}}} \]
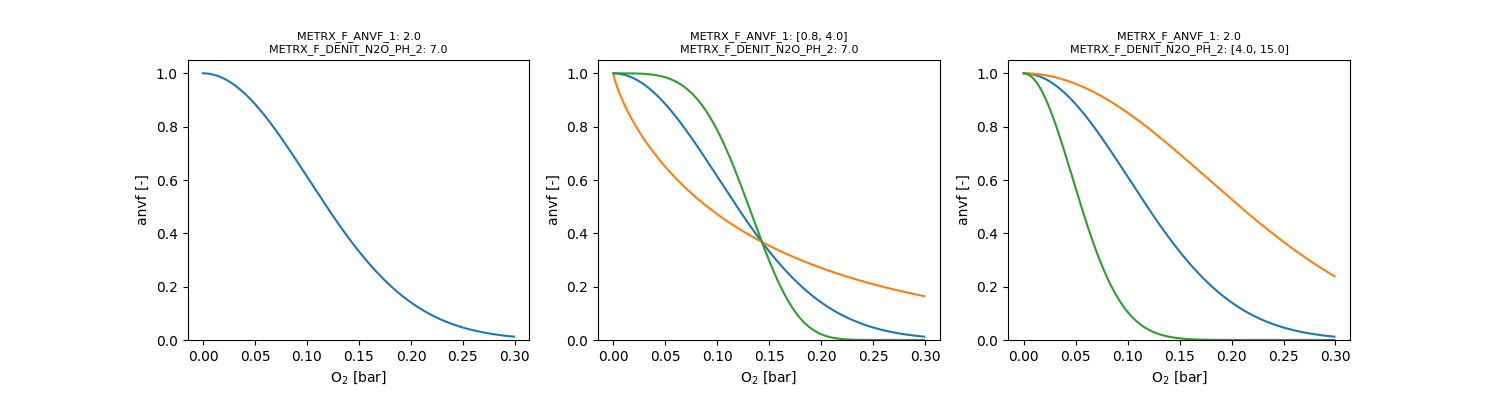
Calibration of both parameters should be restricted to parameter pairs, which yield a response value < 0.2 for partial oxygen pressures at atmospheric conditions.
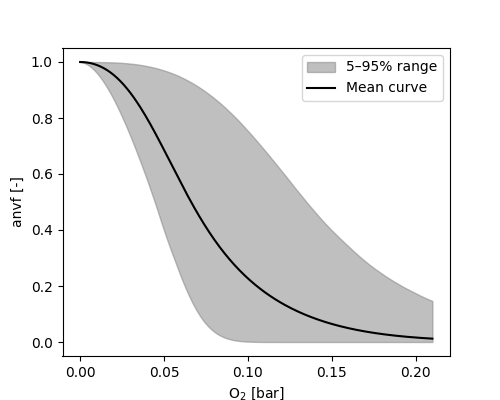
A change of the size of the anaerobic volume induces redistribution of the aerobic and anerobic part of carbon and nitrogen species.
Redistribution occurs by:
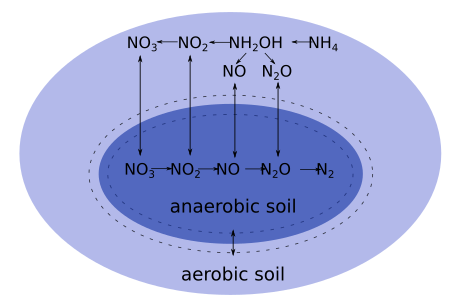
The relative change of a species \( c_x \) only takes place if the share between aerobic and anaerobic volume changes:
\[ \frac{\partial c_{x,an}}{\partial t} = \frac{c_{x,an}}{V_{an}} \frac{\partial V_{an}}{\partial t} \]
\[ \frac{\partial c_{x,ae}}{\partial t} = -\frac{\partial c_{x,an}}{\partial t} \]
The active transport of a species \( c_x \) is given by:
\[ \frac{\partial c_{x,an}}{\partial t} = T^{\ast} \left ( c_{x,an} - c_{x,tot} \frac{V_{an}}{V_{tot}} \right ) \]
\[ \frac{\partial c_{x,ae}}{\partial t} = -\frac{\partial c_{x,an}}{\partial t} \]
The transport coefficient \( T^{\ast} \) is determined by the two parameters:
for gaseous and dissolved species, respectively.
MeTrx considers the following list of synthetic fertilizer:
MeTrx considers the following list of organic fertilizer:
Within the given tilling depth, the following effects are considered:
Urea from fertilizer or manure is dissolved to ammonium in soil and/or in the surface water table depending on temperature:
\begin{eqnarray*} \frac{d NH_4^+}{dT} = N_{urea} \phi_T \\ \frac{d N_{urea}}{dT} = - \frac{d NH_4^+}{dT} \end{eqnarray*}
Depending on the rate of urea hydrolysis, the pH value from of the respective soil layer or water table layer is increased:
\[ pH = pH_i + \frac{\frac{d N_{urea}}{dT}}{METRX\_KMM\_PH\_INCREASE\_FROM\_UREA} \]
with \( p_i \) representing the basi pH value that has been defined as model input.
| entity name | decription | unit |
|---|---|---|
| anvf | Anaerobic volume fraction averaged over the complete soil profile | [-] |
| pore_connectivity | Pore connectivity averaged over the complete soil profile | [-] |
| permeability | Permeability averaged over the complete soil profile | [-] |
| wfps | Water filled pore space averaged over the complete soil profile | [-] |
| air | Water filled pore space averaged over the complete soil profile | [-] |
| root_conductivity | Root conductivity averaged over the complete soil profile | [m2s-1] |
| o2 | Sum of oygen mass over the complete soil profile | [kgha-1] |
| t_eff_crnf | ... | [oC] |
| n_release_fraction_crnf | ... | [-] |
| nitrification_inhibition | Inhibition of nitrification | [-] |
| urease_inhibition | Inhibition of urease hydrolysis | [-] |
| carbon_use_efficiency | Carbon use efficiency | [-] |
| N_don | Sum of dissolved organic nitrogen mass over the complete soil profile | [kgha-1] |
| N_nh4 | Sum of ammonium mass over the complete soil profile | [kgha-1] |
| N_nh4_clay | Sum of ammonium adsorbed to clay minerals mass over the complete soil profile | [kgha-1] |
| N_urea | Sum of urea mass over the complete soil profile | [kgha-1] |
| N_no2_ae | Sum of aerobic NO2 mass over the complete soil profile | [kgha-1] |
| N_no2_an | Sum of anaerobic NO2 mass over the complete soil profile | [kgha-1] |
| N_no3_ae | Sum of aerobic NO3 mass over the complete soil profile | [kgha-1] |
| N_no3_an | Sum of anaerobic NO3 mass over the complete soil profile | [kgha-1] |
| N_n2o_ae | Sum of aerobic N2O mass over the complete soil profile | [kgha-1] |
| N_n2o_an | Sum of anaerobic N2O mass over the complete soil profile | [kgha-1] |
| N_no_ae | Sum of aerobic NO mass over the complete soil profile | [kgha-1] |
| N_no_an | Sum of anaerobic NO mass over the complete soil profile | [kgha-1] |
| N_nh3_gas | Sum of gaseous ammonia mass over the complete soil profile | [kgha-1] |
| N_nh3_liq | Sum of dissolved ammonia mass over the complete soil profile | [kgha-1] |
| C_doc_ae | Dissolved organic carbon (aerobic soil volume) | [kgCha-1] |
| C_doc_an | Dissolved organic carbon (anaerobic soil volume) | [kgCha-1] |
| C_acetate | Acetate | [kgCha-1] |
| C_ch4_gas | Methane in gas phase | [kgCha-1] |
| C_ch4_liq | Dissolved methane | [kgCha-1] |
| C_aorg | Amount of carbon in active organic material pool | [kgCha-1] |
| N_aorg | Amount of carbon in active organic material pool | [kgNha-1] |
| C_micro_1 | Amount of carbon in microbial pool 1 | [kgCha-1] |
| C_micro_2 | Amount of carbon in microbial pool 2 | [kgCha-1] |
| C_micro_3 | Amount of carbon in microbial pool 3 | [kgCha-1] |
| N_micro_1 | Amount of nitrogen in microbial pool 1 | [kgNha-1] |
| N_micro_2 | Amount of nitrogen in microbial pool 2 | [kgNha-1] |
| N_micro_3 | Amount of nitrogen in microbial pool 3 | [kgNha-1] |
| C_humus_1 | Amount of carbon in humus pool 1 | [kgCha-1] |
| C_humus_2 | Amount of carbon in humus pool 2 | [kgCha-1] |
| C_humus_3 | Amount of carbon in humus pool 3 | [kgCha-1] |
| N_humus_1 | Amount of nitrogen in humus pool 1 | [kgNha-1] |
| N_humus_2 | Amount of nitrogen in humus pool 2 | [kgNha-1] |
| N_humus_3 | Amount of nitrogen in humus pool 3 | [kgNha-1] |
| C_litter_soil_1 | Amount of carbon in soil litter pool 1 | [kgCha-1] |
| C_litter_soil_2 | Amount of carbon in soil litter pool 2 | [kgCha-1] |
| C_litter_soil_3 | Amount of carbon in soil litter pool 3 | [kgCha-1] |
| N_litter_soil_1 | Amount of nitrogen in soil litter pool 1 | [kgNha-1] |
| N_litter_soil_2 | Amount of nitrogen in soil litter pool 2 | [kgNha-1] |
| N_litter_soil_3 | Amount of nitrogen in soil litter pool 3 | [kgNha-1] |
| C_algae | Amount of carbon in algae pool | [kgCha-1] |
| N_algae | Amount of nitrogen in algae pool | [kgNha-1] |
| C_litter_stubble | Amount of nitrogen in stubble pool | [kgCha-1] |
| N_litter_stubble | Amount of nitrogen in stubble pool | [kgNha-1] |
| C_total | Total soil organic carbon | [kgCha-1] |
| N_total | Total soil organic nitrogen | [kgNha-1] |
| soc_20cm | Soil organic carbon content in the top 20 cm soil horizon | [%] |
| soc_40cm | Soil organic carbon content in the top 40 cm soil horizon | [%] |
| totn_20cm | Total nitrogen content in the top 20 cm soil horizon | [%] |
| totn_40cm | Total nitrogen content in the top 40 cm soil horizon | [%] |
| fe2_tot | ... | [] |
| fe3_tot | ... | [] |
| till_fact | ... | [] |
| freeze_thaw_fact | ... | [] |
| height_litter | Height of the surface litter layer | [m] |
| ph_watertable | ... | [] |
| ph_soil_surface | ... | [] |
| dN_no3_groundwater | ... | [] |
| dN_assi | ... | [] |
| dN_nit_nh4_no2 | ... | [] |
| dN_nit_no2_no3 | ... | [] |
| dN_nit_no2_no | ... | [] |
| dN_nit_no2_n2o | ... | [] |
| dN_denit_no3_no2 | ... | [] |
| dN_denit_no2_no | ... | [] |
| dN_denit_no2_n2o | ... | [] |
| dN_denit_no2_n2 | ... | [] |
| dN_denit_no_n2o | ... | [] |
| dN_denit_no_n2 | ... | [] |
| dN_denit_n2o_n2 | ... | [] |
| dN_chemodenit_no2_no | ... | [] |
| dC_ch4_oxidation | ... | [kgCha-1] |
| dC_ch4_production_hydrogen | ... | [kgCha-1] |
| dC_ch4_production_acetate | ... | [kgCha-1] |
| dC_floor_ch4_plant_diffusion | ... | [kgCha-1] |
| dC_floor_ch4_soil_diffusion | ... | [kgCha-1] |
| dC_floor_ch4_water_diffusion | ... | [kgCha-1] |
| dC_floor_ch4_bubbling | ... | [kgCha-1] |
| dC_leach_ch4 | ... | [kgCha-1] |
| dO_floor_o2_plant_diffusion | ... | [] |
| dC_litter_above | ... | [kgCha-1] |
| dC_litter_below | ... | [kgCha-1] |
| dC_fix_algae | ... | [kgCha-1] |
| dN_fix_algae | ... | [] |
| dC_decomp_litter | ... | [kg:ha-1] |
| dC_co2_prod_mic_1_growth | ... | [kgCha-1] |
| dC_co2_prod_mic_1_maintenance | ... | [kgCha-1] |
| dC_co2_prod_mic_2 | ... | [kgCha-1] |
| dC_co2_prod_mic_3_acetate_prod | ... | [kgCha-1] |
| dC_co2_prod_mic_3_acetate_cons | ... | [kgCha-1] |
| dC_co2_prod_ch4_prod | ... | [kgCha-1] |
| dC_co2_prod_ch4_cons | ... | [kgCha-1] |
| dH_hydrogen_prod | ... | [] |
| dC_acetate_prod | ... | [kgCha-1] |
| dC_acetate_cons_fe3 | ... | [kgCha-1] |
| dH_hydrogen_cons_fe3 | ... | [] |
| dC_doc_prod_litter | ... | [kgCha-1] |
| dC_doc_prod_humus | ... | [kgCha-1] |
| dC_doc_prod_aorg | ... | [kgCha-1] |
| dC_doc_prod_plant | ... | [kgCha-1] |
| dC_doc_prod_total | ... | [kgCha-1] |
| dC_humify_mic_hum_2 | ... | [kgCha-1] |
| dC_humify_hum_1_hum_2 | ... | [kgCha-1] |
| dC_humify_hum_2_hum_3 | ... | [kgCha-1] |
| entity name | decription | unit |
|---|---|---|
| N_nh4 | Ammonium | [kgNm-2] |
| N_no3 | Nitrate | [kgNm-2] |
| C_doc | Dissolved organic carbon | [kgCm-2] |
| sC_ch4_ebul | CH4 emissions via ebullition | [kgCm-2] |
| sC_ch4_plant | CH4 emissions via plant mediated diffusion | [kgCm-2] |
| sC_ch4_soil | CH4 emissions via soil surface | [kgCm-2] |
| sC_ch4_water | CH4 emissions via surface water table | [kgCm-2] |
| sC_ch4_leach | CH4 leaching | [kgCm-2] |
| sC_ch4_prod | CH4 production | [kgCm-2] |
| sC_ch4_ox | CH4 oxidation | [kgCm-2] |
| sC_acetate_prod | Acetate production | [kgCm-2] |
| sC_doc_prod | DOC production | [kgCm-2] |
| sN_no3_denit | NO3 denitrification | [kgNm-2] |
| sN_n2o_ebul | N2O emissions via ebullition | [kgNm-2] |
| sN_n2o_plant | N2O emissions via plant mediated diffusion | [kgNm-2] |
| sN_n2o_soil | N2O emissions via soil surface | [kgNm-2] |
| sN_n2o_water | N2O emissions via surface water table | [kgNm-2] |
| sN_no_ebul | NO emissions via ebullition | [kgNm-2] |
| sN_no_plant | NO emissions via plant mediated diffusion | [kgNm-2] |
| sN_no_soil | NO emissions via soil surface | [kgNm-2] |
| sN_no_water | NO emissions via surface water table | [kgNm-2] |
| sN_nh3_ebul | NH3 emissions via ebullition | [kgNm-2] |
| sN_nh3_plant | NH3 emissions via plant mediated diffusion | [kgNm-2] |
| sN_nh3_soil | NH3 emissions via soil surface | [kgNm-2] |
| sN_nh3_water | NH3 emissions via surface water table | [kgNm-2] |
| sO_plant_o2_cons | Oxygen consumption by roots | [kgOm-2] |
| sO_plant_o2_prod | Oxygen release by roots | [kgOm-2] |
| sO_algae_o2_prod | Oxygen release by algae | [kgOm-2] |
| ph_watertable | Mean pH value in the surface water table | [-] |
| ph_soil_surface | Mean pH value in the soil | [-] |
| anvf | Anaerobic volume fraction | [%] |
| entity name | decription | unit |
|---|---|---|
| layer | Soil layer | [-] |
| level | Soil layer level (positive from soil surface upwards) | [m] |
| extension | extension | [m] |
| pH | pH value | [-] |
| pore_connectivity | Connectivity of pores | [0-1] |
| relative_permeability | Relative permeability of gaseous diffusion | [0-1] |
| aerenchym_permeability | Aerenchym permeability | [...] |
"cfdd[oC]", water_content | Water content | [0-1] air_content | Air content | [0-1] porosity | Porosity | [0-1] fe2 | Iron Fe2+ [kg:ha-1] fe3 | Iron Fe3+ | [kg:ha-1] C_co2 | CO2 content | [kg:ha-1] C_ch4 | CH4 content | [kg:ha-1] dC_ch4_bubbling | CH4 transport via ebullition | [kg:ha-1] dC_ch4_production | CH4 production | [kg:ha-1] dC_ch4_oxidation | CH4 oxidation | [kg:ha-1] dC_doc_production | DOC production | [kg:ha-1] dC_acetate_production | Acetate production | [kg:ha-1] dC_microbial_death | Microbial death | [kg:ha-1] C_doc | Dissolved organic carbon | [kg:ha-1] C_acetate | Acetate | [kg:ha-1] N_no3 | NO3 | [kg:ha-1] N_nh4 | NH4 | [kg:ha-1] N_urea | IUrea | [kg:ha-1] N_nh3 | NH3 | [kg:ha-1] o2 | Oxygen partial pressure | [bar] N_no | NO content | [kg:ha-1] N_n2o | N2O content | [kg:ha-1] C_humus_1 | Humus pool 1 | [kg:ha-1] C_humus_2 | Humus pool 2 | [kg:ha-1] C_humus_3 | Humus pool 3 | [kg:ha-1] dN_no3_cons_denit | Denitrification of NO3 | [kg:ha-1] denit_factor_c | Factor of denitrification dependency on carbon availability | [0-1] denit_factor_n | Factor of denitrification dependency on nitrogen availability | [0-1] dN_no3_prod_nit | NO3 production from nitrificartion | [kg:ha-1] dN_no3_transport | Downward transport of NO3 | [kg:ha-1]
| entity name | decription | unit |
|---|---|---|
| C_surface | Surface C-litter | [kgCm-2] |
| C_soil_20cm | Total soil carbon in 20 cm topsoil | [kgCm-2] |
| C_humus_1_20cm | Carbon in humus pool 1 in 20 cm topsoil | [kgCm-2] |
| C_humus_2_20cm | Carbon in humus pool 1 in 20 cm topsoil | [kgCm-2] |
| C_humus_3_20cm | Carbon in humus pool 1 in 20 cm topsoil | [kgCm-2] |
| C_litter_20cm | Carbon in litter pools in 20 cm topsoil | [kgCm-2] |
| C_aorg_20cm | Carbon aorg pool in 20 cm topsoil | [kgCm-2] |