 |
LandscapeDNDC
1.36.0
|
|
LandscapeDNDC
1.36.0
|
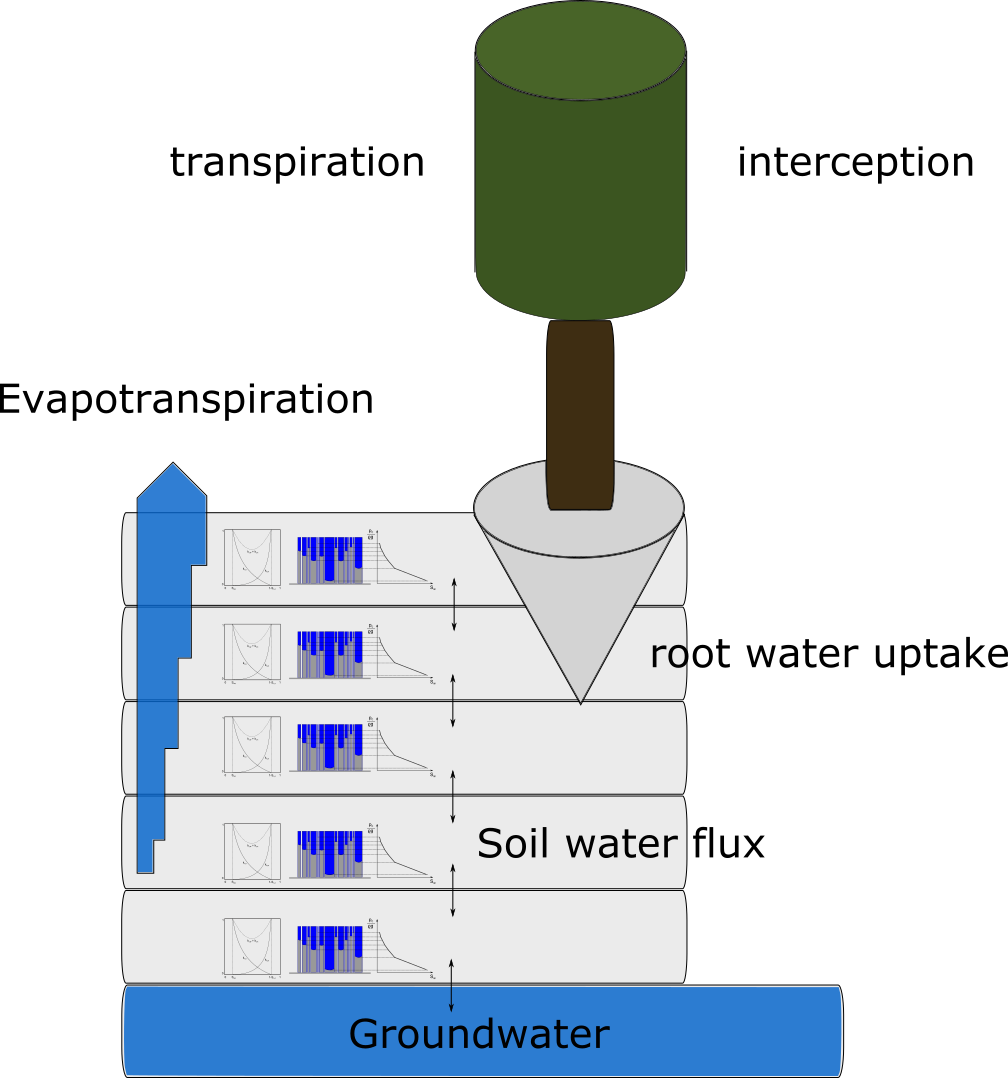
EcHy requires further models for:
The following lists include site parameters that might be calibrated in order to represent the hydrological cycle.
Evapotranspiration:
Interception describes the amount of precipitation, which is hold by the canopy, i.e., not reaching soil surface (see Interception capacity for more details)
Available options: Default options are marked with bold letters.
Actual evapotranspiration is the balance between atmospheric demand of water (potential evapotranspiration) and water supply by the surface. Implemented concepts for the calculation of potential evapotranspiration (default: Thornthwaite):
Evapotranspiration distinguishes evaporation from leaf and soil water as well as transpiration of the prevalent vegetation. While leaf evaporation is not limited, soil evaporation and transpiration depend on:
Soil layer specific transpiration \( TR(z) \) and soil evaporation \( EV(z) \) are given by:
\begin{eqnarray*} TR(z) &=& f_l(\theta) \cdot f_l(m_{fr}) \cdot f_{r,w}(z) \cdot PTR \\ EV(z) &=& f_l(\theta) \cdot f_{e}(z) \cdot PSE \end{eqnarray*}
The factors \( f_l(\theta) \) and \( f_l(m_{fr}) \) refer to limitations due to water availabilty and fine roots abundance, while \( f_{r,w}(z) \) and \( f_{e}(z) \) are distribution factors of total transpiration and evaporation water needs across the soil profile. \(PTR\) and \(PSE\) refer to potential transpiration and soil evaporation, respectively.
Distribution factor for soil layer specific transpiration
Soillayer-specific transpiration depends on fine root abundance \( m_{fr}(z) \) and water availability \( \Delta\theta(z) \). For both, a soil layer specific relative share \( f_{x}(z) \) is calculated and, in a second step, harmonically weighted:
\begin{eqnarray*} f_{r}(z) &=& \frac{m_{fr}(z)}{\sum m_{fr}} \\ f_{w}(z) &=& \frac{\Delta\theta(z)}{\sum \Delta\theta} \\ f_{r,w}(z) &=& \frac{(f_{r}, f_{w})_{harm.}(z)} {\sum (f_{r}, f_{w})_{harm.}} \end{eqnarray*}
Note, \( \sum f_{r} = \sum f_{r} = \sum f_{r,w} = 1 \). Hence respective factors do not limit transpiration but only distribute total transpiration needs across soil layers.
Distribution factor for soil layer specific evaporation
Soillayer-specific evaporation depends on depth:
\begin{eqnarray*} f_d(z) &=& 1 - \frac{z}{z_{limit}} \\ f_e(z) &=& \frac{f_d(z)}{\sum f_d} \end{eqnarray*}
Note, \( \sum f_{d} = \sum f_{e} = 1 \). Hence respective factors do not limit evaporation but only distribute total soil evaporation across soil layers.
Water limitation for transpiration
The reduction of transpiration depending on soil water availability \(\Delta\theta\) is given by:
\[ f_l(\theta) = \frac{\Delta\theta}{\Delta\theta^{\ast}} \]
The reference amount of available water \( \Delta \theta^{\ast} \) that does not limit transpiration is given by the difference between field capacity and wilting point:
\[ \Delta \theta^{\ast} = \theta_{max} - \theta_{min} \]
The amount of available water for transpiration \( \Delta \theta \) is given by:
\[ \Delta \theta = \theta - \theta_{min} \]
Water limitation for soil evaporation
The reduction of soil evaporation depending on soil water availability \(\Delta\theta\) is given by:
\[ f_l(\theta) = \frac{\Delta\theta}{\Delta\theta^{\ast}} \]
The reference amount of available water \( \Delta \theta^{\ast} \) that does not limit soil evaporation is given by the difference between field capacity and residual water content:
\[ \Delta \theta^{\ast} = \theta_{max} - \theta_{r,w} \]
The amount of available water for soil evaporation \( \Delta \theta \) is given by:
\[ \Delta \theta = \theta - \theta_{r,w} \]
Fine roots limitation
The reduction of transpiration depending on fine roots abundance is calculated by a Michaelis-Menten relationship:
\[ f_l(m_{fr}) = \frac{m^l_{fr}}{m^l_{fr} + K_{mm,fr}} \]
The Michaelis-Menten constant is given in the site parameter ECHY_KMM_ROOTS = ECHY_KMM_ROOTS .
Vertical downward movement
Vertical downward movement of water \( q_z \) is calculated via the saturated hydraulic conductivity \( K_f \) and the relative permeability \( k_r \), which depends on water saturation:
\[ q_z = K_f \cdot k_r (\theta) \]
The relative permeability is derived from the van Genuchten soil parametrization following the work of [47] :
\[ k_{r} (\theta_e) = \theta_e \left [ 1 - \left( 1 - \theta_e^{\frac{1}{m}} \right )^m \right ]^2 \]
Effective soil water saturation
The effective soil water saturation ( \( \theta_e \)) linearly scales between the residual water saturation ( \( \theta_e = 0 \)) and the residual air-filled porespace ( \( \theta_e = 1 \)). The residual water saturation is set by default to \( \theta_{r,w} = 0.01 \), while the residual air-filled porespace can be given as model input (default value is set to \( \theta_{r,a} = 0 \)).
Groundwater influence
Percolation within the static groundwater table as given in the model input can be reduced by the site parameter GROUNDWATER_PERCOLATION.
Preferential flow due to, e.g., soil cracks is included by a simple concept, which is based on two parameters representing:
The amount of water that is subject to preferential flow is redistributed within \( z_{pf} \). Soil layers are iteratively filled upwards untill field capacity beginning with the soil layer at \( z_{pf} \).
Snowfall and soil ice formation are calculated as presented in the library functions Snow and ice .
Pore space reduction
Soil ice formation leads to reduction of pore space \( \phi \). Likewise, field capacity \( \theta_{max} \) and wilting point \( \theta_{min} \) are reduced:
\begin{eqnarray*} f(\theta_{ice}) &=& 1 - \frac{\theta_{ice}}{\phi} \\ \theta_{max}^{\ast} &=& \theta_{max} \cdot f(\theta_{ice}) \\ \theta_{min}^{\ast} &=& \theta_{min} \cdot f(\theta_{ice}) \end{eqnarray*}
1.8.13