 |
LandscapeDNDC
1.36.0
|
|
LandscapeDNDC
1.36.0
|
The shape of tree stems is defined by the relation between tree height, diameter and stem volume. While the volume is only constraint by stem biomass and wood density, a change in volume can thus be related to a change in tree height and diameter based on:
Because the taper function is based on tree height and diameter at breast height - but the latter is unavailable for trees shorter than 1.3 m - it is assumed that the form of short trees \((height < 0.5 \cdot HLIMIT)\) is that of a cone. Thus, dimensional growth can be determined from volume growth with only a given height-diameter ratio. The stem volume of large trees \((height > HLIMIT)\) is determined by a taper function.
Both calculations of stem dimensional developments (for short as well as tall trees) require an indication of the optimal height-diameter relationship, which is given as:
\[ hd\_{opt} = (HDMIN + (HDMAX - HDMIN) \cdot exp(-HDEXP \cdot dbh)) \cdot competition\_{factor} \]
\[ competition\_{factor} = (\frac {areacover\_{openrange} }{DFLIMIT} ) ^ {DFEXP} \]
with
If the optimum height:diameter ratio (hd ratio) can be achieved based on the current tree dimensions, it is realized. Otherwise diameter growth will be established iteratively with a hd ratio as close as possible to the optimum one until the new wood volume (vol, m3) matches the calculated volume growth (see taper).
For short trees, a cone-shaped trunk is assumed where the relationship between volume, height, and (base) diameter can be calculated as:
\[ vol_{cone} = \frac {PI \cdot (d\_{base} \cdot 0.5) ^ {2} \cdot height} {3.0} \]
All dimensional changes based on wood volume increase can thus be derived considering the previously defined height-diameter relationship \( f_{hd}(d) \):
\[ height = \frac {vol_{cone} \cdot 3.0} {PI \cdot (d\_{base} \cdot 0.5) ^ {2} } \]
\[ d\_{base} = \frac {height} { hd\_{opt} } \]
with
The taper function that has been selected for the calculation of tree volume [ \(m^3\)] depends on tree height \( h [m] \) and tree diameter \( d [m] \):
\[ vol_{tap} = 0.001 \cdot (100 \cdot dbh)^{TAP\_{P1} } \cdot height^{TAP\_{P2}} \cdot exp(TAP\_{P3}) \]
with
TAP_P1, -P2, P3: species-specific parameters It has been particularly advocated in [14] with parameters for various species (see citation in [65] ).
The taper parameters \( TAP_P1, TAP_P2, TAP_P3 \) are species-specific. Default parameters for coniferous trees are:
Default parameters for deciduous trees are:
According to the taper equation, tree height is can be defined in dependence on tree volume \( V \) [m \(^3\)] and tree diameter at breast height [m]:
\[ height = \left( \frac{vol_{tap}}{0.001 \cdot (100 \cdot dbh)^{TAP_P1}} \cdot exp(TAP_P3) \right)^{\frac{1}{TAP_P2}} \]
Also, tree diameter at breast height can be calculated with this equation based on tree volume \( V \) [m \(^3\)] and tree height [m] using the same taper parameters:
\[ dbh = 0.01 \cdot \left( \frac{vol_{tap}}{0.001 \cdot height^{TAP_P2}} \cdot exp(TAP_P3) \right)^{\frac{1}{TAP_P1}} \]
For larger trees ( \( h > HLIMIT \)), diameter at ground height is determined depending on diameter at breast height \( dbh \) and tree height \( height \):
\( d_{base} = dbh + \frac{HLIMIT}{height} \cdot dbh \)
For \( \; 0.5 \cdot HLIMIT < height \le HLIMIT \; \) a linear transition between the two shapes is assumed:
\[ vol = \phi \; vol_{tap} + (1.0 - \phi) \; vol_{cone} \]
with \( \phi \) representing a linear scaling factor. Accordingly, the diameter used for allometric scaling (e.g. regarding height/diameter ratio) is shifting during this period between ground height (dbase) and breast height (dbh), and is regarded as effective tree diameter ([11]). As described for the volume, the effective tree diameter is defined by a linear transition using the scaling factor \( \phi \)):
\[ d_{eff} = (1 - \phi) \; d_{base} + \phi \; dbh \]
Since the optimum height-diameter ratio might not be achievable given the dimensions of the previous state, a change in trunk volume is translated into height and diameter changes iteratively:
\begin{eqnarray*} d_{test} = DBHLIMIT \\ \text{while} \; (vol_{test} < vol): \\ height_{test} &=& d_{test} \cdot hd\_{opt}(d_{test}) \\ vol_{test} &=& V(d_{test}, height_{test}) \\ d_{test} &=& d_{test} + increment \end{eqnarray*}
With the increment used for diameter modification is plus or minus 10, 1, and 0.5 cm steps.
The crown is generally described by crown length, diameter and a shape function that defines the extension of the crown in each canopy layer. The concept is descript in [21]. The resulting volume is also used to calculate the total demand of branches. Since it is assumed that foliage biomass scales linearly with crown volume, the shape function used to describe the relative canopy volume of each layer and the foliage biomass distribution within the canopy is the same. It is documended under veglibs_biomass_distribution.
The branch fraction is used to calculate the stem biomass and volume that is needed for tree dimensional growth (Dimensional growth). It is EITHER defined using the crown size by assuming a specific branch density per unit volume (Branch fraction from canopy volume) or based on species-specific limit values (Branch fraction from stem diameter). See option settings in Model options.
The crown volume is calculated assuming that every layer can be described as a disc with a horizontal extension defined by the biomass distribution function veglibs_canopy. The total volume can then be integrated across all canopy layers.
\[ f\_{branch} = \frac {m\_{branch} } { (m\_{stem} + m\_{branch}) } \]
\[ m\_{branch} = DBRANCH \cdot can\_{vol} \]
\[ can\_{vol} = \int ( ( \frac {fFol_{fl} } {fFol\_{max} } \cdot crown\_{diam} )^{2} \cdot PI \cdot 0.25 \cdot hfl_{fl} ) \]
with:
If this option is selected (Model options), the branch fraction is empirically related to stem diameter at breast height (dbh). Since the development of this term is different in young seedlings (where no dbh is available) and mature trees, branch fraction is calculated as the maximum of two functions:
\[ f\_{branch} = max(fbranch\_{young}, fbranch\_{mature}) \]
For young trees, a maximumum value is intiated that decreases steeply with increasing size, expressed as diameter at ground height.
\[ fbranch\_{young} = FBRAF\_{Y} \cdot ( 1.0 - exp( FSLOPE\_{Y} \cdot dbas) )^{FEXP\_{Y}} \]
After a minimum branch fraction has reached, it is slowly increasing again approaching a final value for mature trees.
\[ fbranch\_{mature} = FBRAF\_{M} + (1.0 - FBRAF\_{M}) \cdot exp(FSLOPE\_{M} \cdot \frac {dbh}{DIAMMAX} ) \]
with
Crown diameter calculation is based on the open-range calculations that depend on breast-height diameter and tree height as presented by Condes and Sterba [11].
\[ crown\_{diam} = CDR\_{P1} + (CDR\_{P2} \cdot log(dbh)) + (CDR\_{P3} \cdot log(height)) \]
with
In case that the canopy coverage of crowns calculated for open-grown trees is larger that a predefined species-specific threshold value (MORDCROWD), the crown diameter is reduced by a reduction factor that restricts the coverage to the threshold.
For all vegetation types other than woody species, crown length is equal to height. For trees, it is calculated depending on the setup-option selected (options depicted in 'PSIM' descriptions).
The first option is to calculate crown length based on an allometric relationship to tree height and diameter at breast height (= option height):
\[ crown\_{length} = min(HLIMIT, height\_{eff} \cdot CB ) \]
\[ height\_{eff} = height - HREF \cdot (1.0 - \frac {dbh}{DIAMMAX} ) \]
with: \( \text{h}_{\text{cs}} \): height at canopy start
\( \text{h}_{\text{max}} \): height at canopy top
\( DIAMMAX \): tree diameter at which a mature state is defined
\( CB \): relation between crown base height and top height at a mature state (dbh >= DIAMMAX)
\( HREF \): tree height at which crown base height starts to increase
The second option is to calculate crown length from crown diameter (option 'diameter') according to [56] .
\[ crown\_{length} = CL\_{P1} \cdot ( crown\_{diam} ) ^ {CL\_{P2} } \]
with:
Crown length is limited by tree height. The crown base height (or crown start) is defined as tree height - crown length.
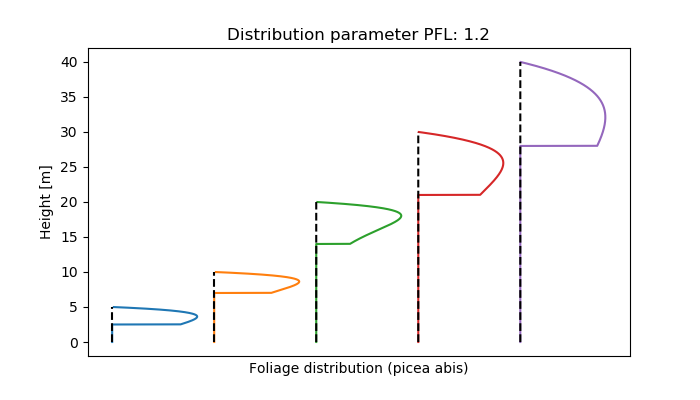
The distribution of foliage biomass \( m(z) \) within the canopy depends on canopy length with a tendency to put more weight to the bottom of the distribution with larger length ([24], [25]):
\[ m(z) = M \cdot \frac{r_{ih} f(z)}{\int r_{ih} f(z)} \\ r_{ih} = \frac{CL - z}{CL} \\ f(z) = p^{100 \frac{z}{CL^2}} \]
\( CL \): canopy length (difference between start and end of canopy, m)
\( z \): distribution depth for which the percentage foliage should be defined (between 0-1, refers to canopy start and top height)
\( p \): shape parameter
Root distribution and root properties are generally fixed throughout the simulation period. Only, if the initial condition of planting doesn't allow the soil profile to be fully rooted (e.g. plants are too small), rooting depth increases linearly with \( GZRTZ \) until the maximum root depth (defined by the soil profile) is reached ( \( ZRTMC \)).
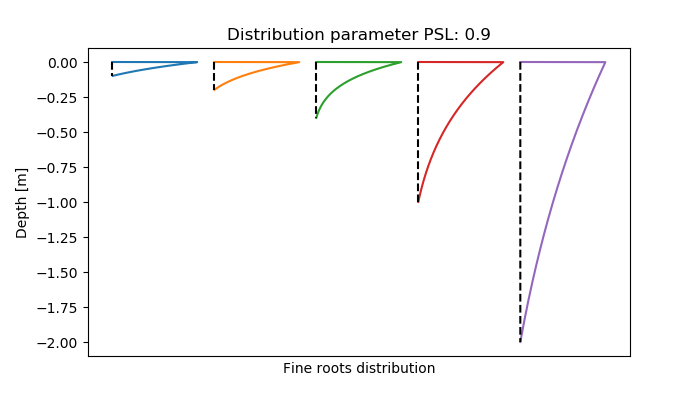
The distribution of fine root biomass \( m(z) \) within the rooting space depends on the rooting depth and is calculated with the same empirical equation as the foliage biomass (veglibs_canopy). The main difference is that the parameter 'p' is generally below 1 now to get a concave distribution ([21]).
\[ m(z) = M \cdot \frac{r_{ih} f(z)}{\int r_{ih} f(z)} \\ r_{ih} = \frac{RD - z}{RD} \\ f(z) = p^{100 \frac{z}{RD^2}} \]
\( RD \): root depth (m)
\( z \): distribution depth for which the percentage roots should be defined (between 0-1, from upper soil boundary to rooting depth)
\( p \): shape parameter
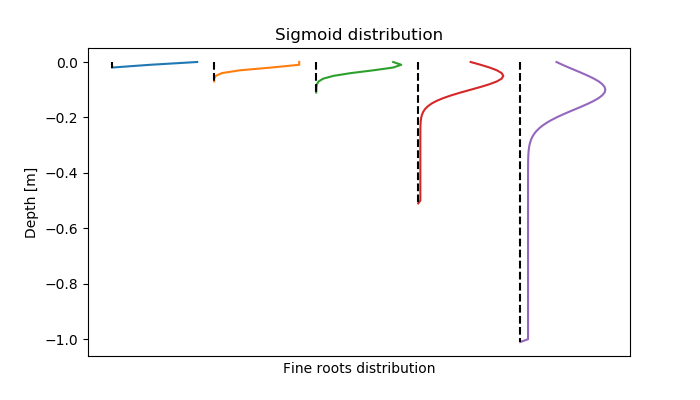
The root distribution decreases sigmoidel with the soil depth:
\[ m(z) = M \cdot \frac{f(z)}{\int f(z)} \\ f(z) = \left( \frac{e^{(-\frac{(z - 0.1 \cdot RD)^2}{0.01 \cdot RD}}}{RD} + 0.1 \cdot L \right) \]
with \( M \): root growth (kg m-2)
\( RD \): root depth (m)
\( z \): distribution depth for which the percentage roots should be defined (between 0-1, from upper soil boundary to rooting depth)
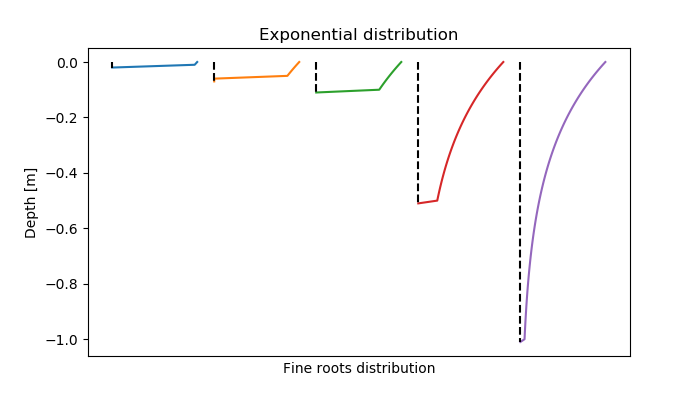
The root distribution decreases exponentially with the soil depth:
\[ m(z) = M \cdot \frac{f(z)}{\int f(z)} \\ f(z) = \exp(-EXP\_ROOT\_DISTRIBUTION \cdot z) \]
with: \( M \): root growth (kg m-2)
\( z \): distribution depth for which the percentage roots should be defined (between 0-1, from upper soil boundary to rooting depth)
\( EXP\_ROOT\_DISTRIBUTION \): species-specific distribution parameter
The function is entered with total carbon allocated to the roots (with costs for growth respiration alread considered before), and it is then decided where to put the new biomass according to specific rules. There is no active redistribution of old root biomass but root biomass which is not supported by growth will continously decrease due to senescence.
If no other options are defined, new root biomass is distributed to the different soil layers according to the selected root distribution scheme (standard, sigmoidal, or exponential). Therefore, the overall distribution stays constant.
Carbon distribution to roots is based on previous nitrogen uptake of a particular layer. Thus, roots grow stronger in soil layers with high nitrogen availability.
Root biomass distribution may be limited by various influences that prevent the realization of a particular distribution scheme. Based on an optimum root biomass distribution assuming either exponential or sigmoidal functions, these restrictions are calculated separately for all relevant layers, following [3].
Sink driven allocation starts and ends with germination period. Outside this period, carbon distribution is done empirically. The different restrictions within the relevant period are considered as follows:
Update rooting depth
I Restrictions due to coarse fragments
\[ S_{Fc}(sl) = 1 - stone\_content [\text{volume fraction}](sl) \]
with
II Restrictions due to bulk density The bulk density enters via \(S_{BD}\), which is given by
\[ S_{BD} = 1, \quad BD < BD_O\,,\\ S_{BD} = \frac{BD_X-BD}{BD_X-BD_O}, \quad BD_O \leq BD \leq BD_X\,,\\ S_{BD} = 0, \quad BD > BD_X\, , \]
where the threshold \(BD_O\) is the bulk density at which root growth is first affected, and \(BD_X\) is the bulk density above which no root growth occurs. Following [3], these parameters can be estimated from the sand content [weight fraction] \(sand\)
\[ BD_O = 1.1 + 0.005 \cdot sand\, ,\\ BD_X = 1.6 + 0.004 \cdot sand\, . \]
III Restrictions due to poor aeration Plants do not have any stress if the water filled porosity is below a critical value, whereas above this critical value the stress factor scales linearly between 1 and 0 in a fully saturated soil.
\[ S_{AI} = S_{FT} + (1- WFP) \cdot \frac{1- S_{FT}}{1 - CWP}, \quad WFP \geq CWP \,,\\ S_{AI} = 1, \quad WFP < CWP \,. \]
With the fraction of water filled pore space calculated as:
\[ WFP = \frac{\text{water filled porosity}}{\text{total porosity}} \]
The critical value of water filled pore space depends on the clay content:
\[ CWP = 0.4 + 0.004 \cdot clay \, . \]
IV Restriction due to temperature stress If the soil temperature is below a critical value ($T_{BS}$), root growth doesn't occur. Similar, too hot conditions also restricted carbon allocation into roots. Here, it is assumed that the limitations occur symmetrically around an species-specifc optimum temperature $T_{OP}$, using a sinus function around an optimum temperature to describe the dependency.
\[ S_{TP} = 0, \quad T<T_{BS} \,,\\ S_{TP} = \sin\left( \frac{\pi}{2} \frac{T-T_{BS}}{T_{OP}-T_{BS}}\right), \quad T_{BS} \leq T \leq 2T_{OP} - T_{BS}\,,\\ S_{TP} = 0, \quad T > 2T_{OP} - T_{BS}\,. \]
V Restriction due to flooding In addition, a species-(or genotype-)specific sensititivity to flooding \(S_{FT}\) is introduced.
\[ S_{FT} = 0, \quad \text{corn, maize, soybean, etc.} \,,\\ S_{FT} = 1, \quad \text{rice, etc.} \,. \]
The combination of individual restrictions is then done following [3] :
\[ \Delta rd_{red} = \Delta rd_{pot} \cdot \min\left(STP, \min(SST,SAI,SCF)^{0.5} \right), \]
The restrictions in the bottom layer are assumed to represent a reasonable simplification as long as the time steps are small so that root elongation is also small in comparison to the soil layer widths.
While root biomass is defined by one of the rooting distribution schemes, root length is calculated based on root biomass but considering a specific root length for every single soil layer. Specific root lenghts scales linearly between \(SRLMIN\) and \(SRLMAX\) as:
\[ specific\_{rootlength}_{sl} = SRLMAX - dvsFlush \cdot (SRLMAX - SRLMIN) \cdot scale_{sl}; \]
\[ scale = 1.0 - \frac {depth_{sl}} {depth\_{root}} \]
with
Assumptions:
Ratio between sapwood and foliage area (Huber Value) The sapwood to foliage area relationship (m2 sapwood area m-2 leaf area) is calculated following [36], which is assumed to scale linearly with tree height.
\[ qsfa = QSF\_{P1} + height \cdot QSF\_{P2} \]
with
Vernalization after [27].
Influence of vernalization starts as soon as accumulated growing degree days \( AGDD \) are greater than half of the required growing degree days for the state of flowering \( GDD\_FLOWERING \):
\[ AGDD > 0.5 \cdot GDD\_FLOWERING \]
Chill factor \( f_{chill} \) is given by:
\[ f_{chill} = 1 - \frac{AGDD - 0.5 \cdot GDD\_FLOWERING}{0.5 \cdot GDD\_FLOWERING} + \frac{ACU}{CHILL\_UNITS} \]
wherein \( ACU \) and \( CHILL\_UNITS \) refer to accumulated chill units and required chill units for complete vernalization, respectively. The factor \( f_{chill} \) is bound between 0 and 1.
Accumulated chilling units \( ACU \) are given by:
\begin{eqnarray*} ACU &=& \sum CU \\ CU &=& \frac{CHILL\_TEMP\_MAX - T_{avg}}{CHILL\_TEMP\_MAX} \end{eqnarray*}
\( CHILL\_TEMP\_MAX \) and \( T_{avg} \) refer to a species-specific parameter and daily mean temperature, respectively.
Exponential drought stress factor \( \phi_d \):
\[ \phi_d = \frac{1 - e^{-f_{H2O} gsslope}}{1 - e^{-gsslope}} \]
Related literature: Soil drought impact on stomatal conductance [59]
\[ \phi_d = 1.016 - 0.016 \cdot e^{ 4.1 \cdot ( 1.0 - _fh2o)} \]
A general relationship for 5 tree species was developed by [19]
\[ \phi_d = (1.154 + 3.0195 \cdot _fh2o - ((1.154 + 3.0195 * _fh2o)^2 - 2.8 \cdot 1.154 \cdot 3.0195 \cdot _fh2o)^{0.5}) /1.4)); \]
Linearly calculated soil drought impact on stomatal conductance ( \( \phi_d \)) according to [62] (more flexible due to species-specific sensitivity):
\[ \phi_d = min \left ( \frac{f_{H2O}}{f_{H2O,ref}} , 1 \right ) \]
Non-stomatal impact of drought stress (Tuzet et al. 2003)
1.8.13