WatercycleDNDC

Table of Contents

• User guide
  • Model structure
  • Parametrization
• Model options
• Management
  • Irrigation
  • Flooding
• Rainfall distribution
• Snow and ice
• Potential evapotranspiration
• Interception
• Transpiration
  • Model options /n
  • Minimum rule
  • Transpiration after Couvreur
• Evaporation
  • Evaporation from surface water
  • Snow evaporation
  • Soil water evaporation
• Soil water flow
  • Infiltration
  • Groundwater interaction
  • Water flow at bottom
  • Water flow within domain
    • Water flow above field capacity
    • Water flow below field capacity
    • Capillary rise
    • Preferential flow
    • Impedance
• Surface runoff

User guide

This WatercycleDNDC model is taken from the PnET-N-DNDC Model (Li 2000). It calculates daily dynamics of snowcover, soil ice content, potential evaporation and hourly dynamics of rainfall, interception, transpiration, percolation, and runoff.

Watercycle overview

Model structure

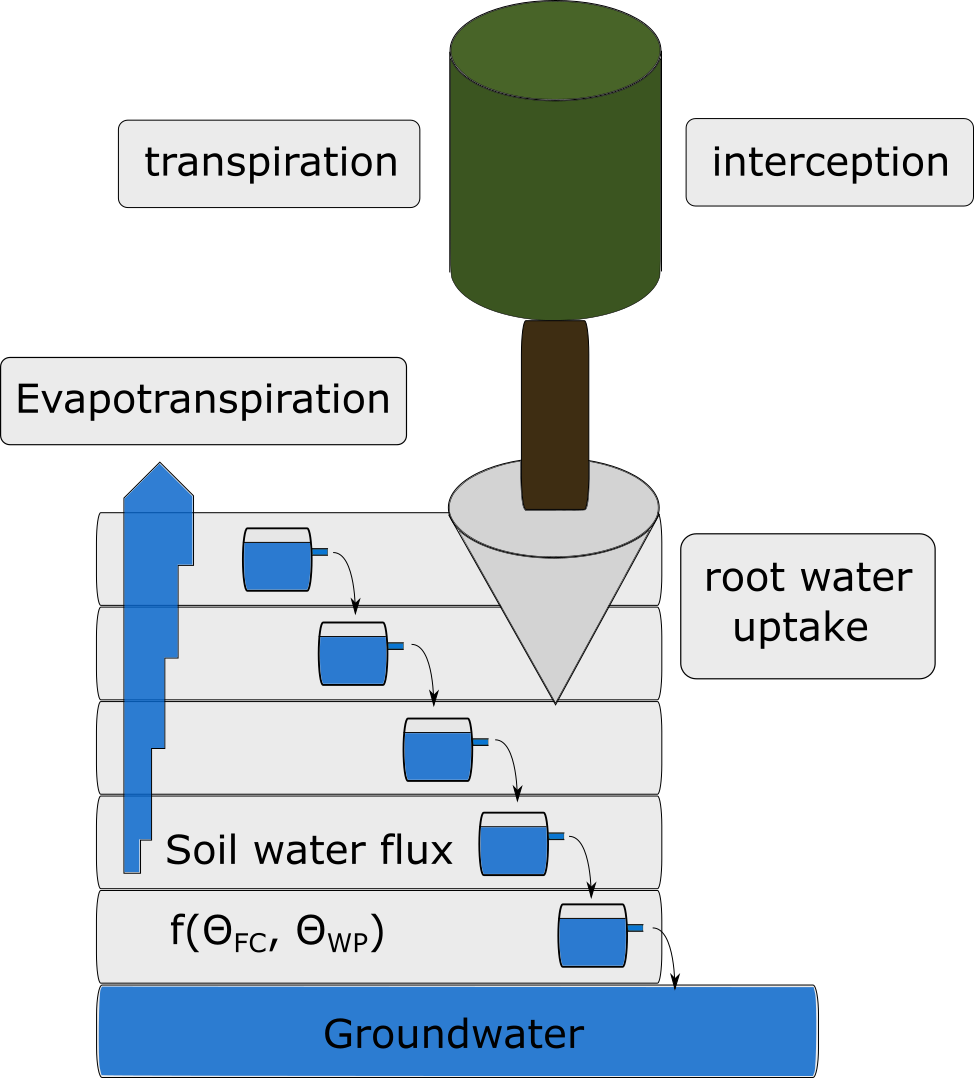
WatercycleDNDC requires further models for:

• plant growth (e.g., transpiration demand, fine roots distribution)

Parametrization

The following lists include parameters that might be calibrated in order to adapt the model to site conditions:

Interception:

• MWWM (speciesparameter: specific interception capacity of wood mass (m kg-1DW))
• MWFM (speciesparameter: specific interception capacity of foliage (m m-2LAI))

Evapotranspiration:

• \( ROOT\_DEPENDENT\_TRANS \)
• \( WCDNDC\_INCREASE\_POT\_EVAPOTRANS \)

Preferential flow

• \( BY\_PASSF \)

Lateral runoff

• \( FRUNOFF \)

Percolation

• \( FPERCOL \)
• \( IMPEDANCE\_PAR \)

Model options

Available options: Default options are marked with bold letters.

• Potential evapotranspiration model (default: "potentialevapotranspiration" = thornthwaite / penman, priestleytaylor)
• Automatic irrigation (default: "automaticirrigation" = -1.0) Set to a number \( x \) within the interval [0.0, 1.0] in order to automatically trigger irrigation as soon as the soil water content \( wc \) drops below a defined target water content depending on wilting point \( wp \) and field capacity \( fc \):

  \[ wc < wp + x (fc - wp) \]

Management

Irrigation

Irrigation events are simply added to rainfall.

Flooding

Selectable flooding regimes via event input:

• Continuous surface water and fully saturated soil profile
  • Constant height of surface water table (set only: watertable > 0.0).
  • Minimum height of surface water table, e.g., precipitation can lead to higher surface water (set: watertable > 0.0 and bundheight > watertable).
  • Minimum height of surface water table, e.g., automatic irrigation as soon as defined minimum surface water is reached (set: watertable > 0.0 and irrigationheight > watertable).
• Alternating wetting and drying: Automatic irrigation as soon as soil water table drops below defined value. The specified value must be negative since it corresponds to a soil water depth below ground level. (set: watertable < 0.0 and irrigationheight > 0.0).
• Moist soil conditions: Soil layers above a specified depth are continuously set to field capacity, while soil layers below are set fully water saturated (set only watertable < 0.0)
• Fixed bund height (bundheight > 0.0 ). Water table is calculated dynamically depening on water input (precipitation & irrigation)
• Percolation rate (percolationrate > 0.0). Maximum value for soil water percolation. Can be defined in order to reflect soil puddling, which decreases soil water percolation under flooded conditions.

Rainfall distribution

Rainfall per timestep set by a parameterized rainfall intensity (RI, mm timestep-1). Thus, the number of timesteps (usually hours) with rainfall is given by:

\[ nts_{rain} = \frac {P}{RI} \]

with

• P: precipitation (mm day-1)

If the precipitation per day is larger than the parameterized rainfall intensity times the number of timesteps, rainfall intensity will be increased accordingly:

\[ ri_{act} = \frac { P }{ n_{timesteps} } \]

with

• n_timesteps: number of timesteps per day

Snow and ice

Snowfall and soil ice formation are calculated as presented in the library functions Snow and ice .

Potential evapotranspiration

Actual evapotranspiration is the balance between atmospheric demand of water (potential evapotranspiration) and water supply by the surface. Implemented concepts for the calculation of potential evapotranspiration (default: Thornthwaite):

• Thornthwaite
• Priestley and Taylor
• Penman

Interception

Both, rainfall and irrigation are subject to interception. The amount of water that can be intercepted depends on:

• vegetation coverage
• vegetation specific interception capacity

The interception capacity is defined as the moisture quantity a plant species can harbour in the stems and in the foliage system (see Interception capacity).

All water that is not intercepted feeds into surface water from where it either infiltrates into the soil or is subject to lateral runoff.

Intercepted water contributes to total evapotranspiration. Leaf water evaporation equals the minimum of leaf water and potential evapotranspiration.

Remaining leaf water is redistributed depending on leaf area

Transpiration

Update soilwater content due to transpiration.

Model options /n

a) model configuration transpiration = true: water content is updated /n

b) model configuration transpiration = false: water content has been updated by external model

Minimum rule

• The water potentially used for transpiration ( \(pottrans\)) is taken as the minimum value of the potential transpiration (provided by the physiology module, see Potential transpiration) and the potential evaporation (see Potential evaporation), reduced by evaporation of intercepted water. Both potential values are derived as daily averages. Therefore, transpiration occurs in the model also at night.
• Rooting depth and root mass distribution are taken into account.
• The potentially available water in a layer (wc-wcmin) is reduced by soil properties (clay, cord), resulting in an reduced available water amount.

1) By iterating rooted layers, determine:

• the total available soil water for uptake by transpiration
• the total available soil water weighted by soil properties
• the fine root density sum needed for further weighing.

2) Determine the weighted water uptake capacity:

\[ c = \frac{rootdensity_l}{\sum\limits_l rootdensity} \cdot \frac{H2O available for uptake_l}{\sum\limits_l H2O available for uptake} \]

and its sum over all layers.

3) Calculate actual uptake:

\[ up_l = \min( \frac{c}{\sum\limits_l c} * pottrans , H2O available for uptake_l) \]

The soil water reservoirs are decreased accordingly. The routine iterates from top to bottom and stops as soon as the water demand is fullfilled (usually water is taken up from all rooted layers if available).

Transpiration after Couvreur

This function is called if ROOT_WATER_UPTAKE_COUVREUR = true (false) and model configuration transpiration = true.

It updates the soil water content regarding the root water uptake for transpiration. The root water uptake is modeled by the Couvreur model (first derived in 3d [14], 1d in [15], in the notation in Ref. [cai:2018a] for every plant species individually. The potential transpiration is split up for different species by the mass fractions. As species parameters KRSINIT, KCOMPINIT, FRTMASSINIT, and HLEAFCRIT = -16000cm (constant by stomatal regulation) enter.

An effective soil water pressure head ( \( h<0 \) for unsaturated soil, [L][cm]) is determined by

\[ h_{eff} = \sum\limits_{sl=0}^{deepest rooted layer} h(sl) \cdot frcfrts(sl) \]

The water potentials are determined via the van-Genuchten parametrisation.

The hydraulic conductivites of the root system \(K_{rs}\) [m/m/h] and for compensation \(K_{comp}\) [m/m/h] scale linearly with the root biomass in respect to the initial root biomass FRTMASSINIT. The parameters for initialisation relate to the same plant stage/time.

\[ K_{rs} = KRSINIT \cdot m_{frts} / FRTMASSINIT\\ K_{comp} = KCOMPINIT \cdot m_{frts} / FRTMASSINIT\, . \]

They can be understood as the volumetric fraction of water, which is extracted in an hour.

The root water uptake, as the intensive volumentric water fraction [m/m/timestep], from every layer is calculated by

\[ S(sl) = \left( K_{rs} \cdot (h_{eff} - h_{leaf} ) + K_{comp} \cdot (h(sl) - h_{eff}) \right) \cdot \frac{massfrts(sl)/layerwidth}{massallfrts}\, . \]

In contrast to Cai 2017, we therefore use the fine root mass density fractions instead of the normalised root length density.

The potentially used water for transpiration ( \(T_{pot}\)) is provided by another module (physiology). The pressure head of the leaves is derived from the potential transpiration, as long as this value remains above the critical leaf water pressure head HLEAFCRIT.

\[ \tilde h_{leaf} = h_{eff} - \frac{T_{Pot}}{K_{rs}} \]

a) If \(\tilde h_{leaf} > HLEAFCRIT\), it is \(h_{leaf} = \tilde h_{leaf}\), then \(T_{act} = T_{pot} \),

b) otherwise \( h_{leaf} = HLEAFCRIT\), then \( T_{act} < T_{pot} \).

The values wcmin and wcmax are not used with this root water uptake model, but the water potentials related to the Van-Genuchten parameters. In contrast, in PlaMox, for the drought stress factor, which enters photosynthesis, wcmin and wcmax are used. Therefore, if the hydraulic conductivity of the root system is unrealisitcally small, or if the Van-Genuchten parameters are not chosen in accordance to wcmin and wcmax, the actual transpiration can be smaller than the potential transpiration without the photosynthesis being affected from this. The Van-Genuchten parameters and wcmin, wcmax should be initialised consistently in the site file.

Evaporation

Evaporation from surface water

If the potential evapotranspiration (from CalcPotEvapoTranspiration() and reduced by evaporation from intercepted water, transpiration and evaporation from snow) is not yet zero, and if there is water remaining at the surface, water from this remaining surface water evaporates.

If the potential evapotranspiration is larger than the surface water, all the surface water evaporates.

If the amount of surface water is larger than the potential evapotranspiration, the potential evapotranspiration is reached as the actual evapotranspiration and some surface water still remains.

Snow evaporation

Snow decrease from evaporation (original in unit: evaporation_of_snow) Since potential evaporation is 0 at freezing temperatures, snow evaporation occurs only for snow that can not melt fast enough If there is more evaporation than can be expected with the sum of gross potential evaporation, hourly foliage evaporation and hourly transpiration, the remaining evaporation is assumes to occur from the snow surface.

Soil water evaporation

Water from the soil evaporates

• down to \( EVALIM \)
• as long as the water content is above wilting point

  \[ \theta(sl) = WCDNDC\_EVALIM\_FRAC\_WCMIN \cdot \theta_{wp}(sl) \]

• potential evapotranspiration is larger zero

Amount of water evaporating from a soil layer \( sl \) :

\[ \frac{dE}{dT} = \text{bound}\left(0, \frac{potevapotrans}{\text{EVALIM}} \cdot limitwi \cdot \max\left( 0, 1-\frac{\min(\text{EVALIM}, depth(sl))}{\text{EVALIM}} \right), \theta(sl) \cdot limitwi \right) \]

• \( potevapotrans\) : water for potential evapotranspiration
• limiting factor for soil water infiltration \( limitwi \):

  \[ limitwi = \begin{cases} &0, \qquad\qquad\qquad\qquad\qquad \theta(sl) < wcminevap(sl)\\ & \min\left(\left(\frac{wc(sl)-wcminevap(sl)}{wcmax(sl)}\right)^{clayfact}, 1\right), \qquad \text{else} \end{cases} \]

• factor including further soil properties

  \[ clayfact = 1+ SLOPE\_CLAYF \cdot \min\left(1- forg(sl), clay(sl)\right) \]

• \(forg(sl)\): fraction of organic matter

Comments:

• The water available for evapotranspiration is distributed homogeneously over all soil layers from which water potentially evaporates (down to EVALIM). The amount of water actually evaporating from every layer is further reduced linearly with the layer depth.
• Soil water evaporation for every layer takes place after the downwards percolation from that layer.

Soil water flow

Infiltration

For the top soil layer, water inflow equals total surface water. For deeper soil layers, water inflow equals water outflow of the overlying soil layer.

Groundwater interaction

For soil layers lying within the groundwater table, water flow out of the layer equals water inflow. In this way, soil water is discharged with groundwater with the percolation flow rate of the soil layer above the groundwater table.

Water flow at bottom

If the last soil layer is above the groundwater, water flow out of the domain is given by:

1. Fully saturated conditions
   Saturated hydraulic conductivity
2. Water content below saturation and above field capacity ( \(\phi > \theta > \theta_{fc} \))
   Water flow is calculated in the same way as for all other soil layers (see below)
3. Water content between field capacity and wilting point ( \(\theta_{fc} > \theta > \theta_{wp} \))
   Water flow out of the layer is calculated depending on the flow into the layer: \( q_{out} = FPERCOL \cdot q_{in} \)
4. Water content below wilting point ( \(\theta_{wp} > \theta\))
   No flow
   

Water flow within domain

Calculation of water flow ouf of soil layer is distinguished for different water contents:

1. Fully saturated conditions
   Saturated hydraulic conductivity
2. Water content below saturation and above field capacity ( \(\phi > \theta > \theta_{fc} \))
   See Water flow above field capacity
3. Water content between field capacity and wilting point ( \(\theta_{fc} > \theta > \theta_{wp} \))
   See Water flow below field capacity
4. Water content below wilting point ( \(\theta_{wp} > \theta\))
   No flow
   

Water flow above field capacity

Water flow from layer \(sl\) to the layer \(sl+1\) below:

\[ q = \left(1-\frac{\theta_{fc}(sl)}{\theta(sl)}\right)^2 \cdot \theta(sl) \cdot \left(1 - e^{\frac{1}{log(sks)}} \right) \cdot factimpedence \]

Water flow below field capacity

Water flow from layer \(sl\) to the layer \(sl+1\) below:

\[ q = \left(\frac{\theta(sl)}{\theta_{fc}(sl)} - \frac{\theta(sl+1)}{\theta_{fc}(sl+1)} \right) \cdot \theta(sl) \cdot \left(1 - e^{\frac{1}{log(sks)}} \right) \cdot factimpedence \]

Capillary rise

Similar to WaterFlowBelowFieldCapacity but restricts water flow by water availability from soil layer below

Preferential flow

...

Impedance

Percolating water is imepded by an impedance factor, which considers the formation of ice lenses in (partially) frozen soil [Lundin (1990), Hansson et al. (2004).] The impedence factor depends on the parameter IMPEDANCE_PAR = 0.

• If no ice is present the impedence factor is 1 and no reduction occurs.
• If IMPEDANCE_PAR = 0 the impedence factor is 1 as well and no reduction occurs.

Surface runoff

The surface flux gives the water, which runs off horizontally. This only happens if more water than stopped by the bunding (bund height is set in flooding events) is present.

• If the bund height > 0: All water above the bund height runs off immediately.

• If the bund height == 0:

  The fraction of water running off is determined by the site parameter FRUNOFF.

  • If a time step is 24h (daily simulation), FRUNOFF corresponds to the fraction of water running off in these 24h. Hence, FRUNOFF = 1 corresponds to a complete run off, i.e. 100% of the surface water
  • If a time step is 1h (hourly simulation), only the fraction FRUNOFF/24 runs off in this time step, the rest of the water remains as surface water for the next time step. For an hourly time step a complete run off corresponds to FRUNOFF = 24. A run off of 50% would be FRUNOFF=12.